Fysiker använder teoretiska modeller för att studera fysiska storheter, såsom massan av kärnor, där de inte har experimentella data. Att använda en enda ofullkomlig teoretisk modell kan dock leda till missvisande resultat. För att förbättra kvaliteten på extrapolerade förutsägelser kan forskare istället använda flera olika modeller och blanda sina resultat. På detta sätt får forskare ut det mesta av den kollektiva visdomen från flera modeller och får den bästa förutsägelsen från den senaste experimentella informationen.
För att förbättra förutsägbarheten hos komplexa beräkningsmodeller föreslog ett team av kärnfysiker och statistiker en ny statistisk metod. Denna metod använder en statistisk process som kallas Bayes sats för att revidera sannolikheten för en hypotes när nya data erhålls. Arbetet publiceras i tidskriften Scientific Reports .
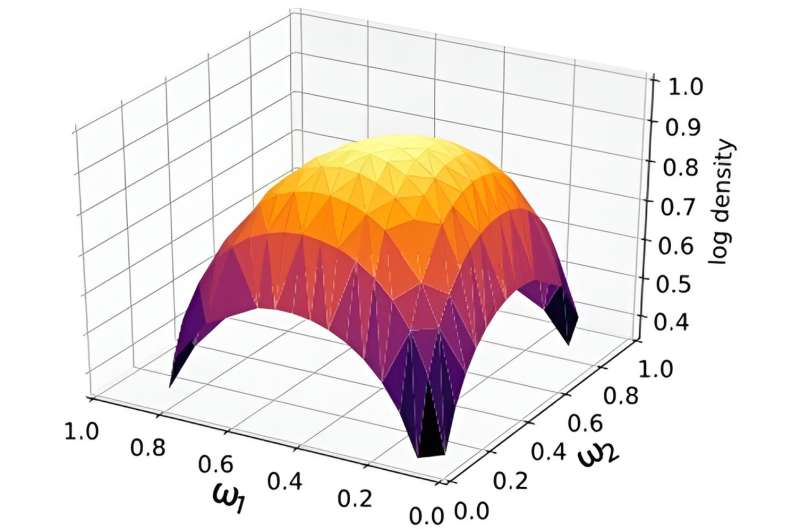
Det resulterande maskininlärningsramverket använder den så kallade Dirichlet-distributionen. Denna statistiska process kombinerar resultaten av flera ofullkomliga modeller. Forskarna visade förmågan hos de föreslagna blandningsteknikerna att bryta data om kärnmassor.
Denna forskning visade att globala och lokala blandningar av modeller har utmärkta prestanda både vad gäller noggrannheten i deras förutsägelser och deras kvantifiering av osäkerhet. Dessa blandningar verkar vara att föredra framför klassisk Bayesiansk modellmedelvärde, det konventionella tillvägagångssättet. Dessutom indikerar forskarnas analys att förbättring av modellförutsägelser genom enkel blandning leder till mer robusta extrapolationer än blandning av korrigerade modeller.
Mer information: Vojtech Kejzlar et al, Local Bayesian Dirichlet mixing of imperfect models, Scientific Reports (2023). DOI:10.1038/s41598-023-46568-0
Journalinformation: Vetenskapliga rapporter
Tillhandahålls av US Department of Energy