Ett team av forskare från University of Ottawa erbjuder insikter i mysterier med kvantförveckling. Deras nyligen genomförda studie, med titeln "Extending the known region of nonlocal boxes that collapse communication complexity" och publicerad i Physical Review Letters (PRL), avslöjar att olika teoretiska kvantteoriutvidgningar anses icke-fysiska när de testas mot principen om icke-trivial kommunikationskomplexitet.
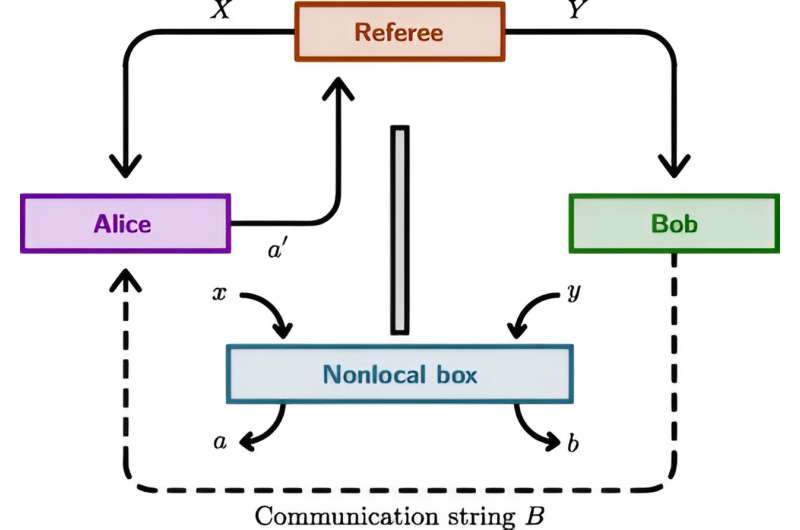
Dessa kvantteoretiska utökningar kan symboliseras av en rad icke-lokala rutor, som är teoretiska anordningar som används för att illustrera vissa aspekter av kvantförveckling och icke-lokalitet.
Studien utfördes av Anne Broadbent, professor och forskningsordförande vid University of Ottawas institution för matematik och statistik, tillsammans med Pierre Botteron, en Ph.D. kandidat från University of Toulouse, Frankrike, som också är gästforskare vid University of Ottawa, och Marc-Olivier Proulx, en MSc-alumn vid Institutionen för fysik vid University of Ottawa.
Kvantmekanikens principer har traditionellt sett varit det viktigaste ramverket för att förstå partikelbeteende och kvanttrassling. Tsirelsons gräns – ett kvantfysikbegrepp som handlar om korrelationer mellan avlägsna partiklar – och dess pålagda restriktioner har dock fått forskare att ifrågasätta om en bredare teori är möjlig.
Detta har gett upphov till icke-lokala rutor, som är teoretiska expansioner av kvantteorin, som ett sätt att utforska en mer holistisk skildring av universum. Denna forskning fokuserar på att använda icke-trivial kommunikationskomplexitet för att bedöma genomförbarheten av icke-lokala boxar.
"Vår forskning förbättrar vår förståelse av begränsningarna och gränserna för utvidgningar av kvantteori och ger insikt i kvantförvecklingens gåtor", säger professor Broadbent.
Kvantförveckling, ett fängslande fenomen som beskrivs av kvantmekaniken, har fått stor uppmärksamhet i det vetenskapliga samfundet. Nobelpriset 2022 tilldelades Aspect, Clauser och Zeilinger för deras banbrytande experiment med intrasslade fotoner, som avslöjade kränkningen av Bells ojämlikheter och banbrytande kvantinformationsvetenskap.
Trots kraften i kvantmekaniken, väcker existensen av Tsirelsons gräns frågan om det finns en mer omfattande teori för att beskriva den naturliga världen korrekt. Denna studie undersöker icke-lokala rutor som potentiella generaliseringar av kvantmekanik, i syfte att fastställa deras fysiska realiserbarhet.
Forskningen inleddes 2018 med Marc-Olivier Proulxs MSc-uppsats, som han genomförde under ledning av professor Anne Broadbent vid University of Ottawa och under medhandledning av avlidne professor David Poulin vid Université de Sherbrooke.
Byggande på detta arbete, Pierre Botteron, en Ph.D. student under professor Broadbent, samarbetade med Proulx för att ytterligare utforska riket av icke-lokala boxar och postulatet om icke-trivial kommunikationskomplexitet. Undersökningen omfattade teoretisk analys och rigorös matematisk modellering baserad på etablerade ramverk och principer inom kvantmekaniken.
"Vår studie avslöjar att många teoretiska generaliseringar av kvantteorin, representerade av olika familjer av icke-lokala lådor, anses icke-fysiska när de utsätts för postulatet om icke-trivial kommunikationskomplexitet. Dessa fynd utökar förståelsen av de begränsningar som generaliseras kvantmekanik. och ge värdefulla insikter om karaktären av quantum intrassling," förklarar professor Broadbent.
Att utforska icke-lokala lådor som en generalisering av kvantmekaniken har förbättrat vårt grepp om kvantteoretiska gränser. Genom att undersöka postulatet om icke-triviala kommunikationskomplexitet har uOttawas forskare upptäckt ett bredare spektrum av generaliseringar som avfärdats som icke-fysiska. Den här forskningen öppnar dörren till framsteg inom kvantinformationsvetenskap och fördjupar vår förståelse av fenomen med kvantförveckling.
Mer information: Pierre Botteron et al, Extending the Known Region of Nonlocal Boxes that Collapse Communication Complexity, Physical Review Letters (2024). DOI:10.1103/PhysRevLett.132.070201. På arXiv :DOI:10.48550/arxiv.2302.00488
Journalinformation: Fysiska granskningsbrev , arXiv
Tillhandahålls av University of Ottawa