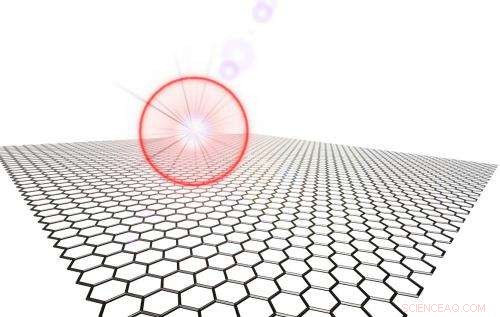
Detta schema visar grafen upplyst av en laser. Genom att interagera med elektroner i grafen, laserfältet kan producera bandluckor i grafenens elektroniska struktur. Bildkredit:Luis E. F. Foa Torres.
(PhysOrg.com) -- En av de mest citerade egenskaperna hos grafen – det tvådimensionella kristallgittret av kol – är dess unika elektroniska egenskaper. Många av dessa elektroniska egenskaper gör grafen attraktivt som material för kolbaserad elektronik. Men även bland dessa egenskaper är att grafen är en gapfri halvledare. Som fysikern Luis Foa Torres förklarar, det faktum att grafen inte har ett bandgap är dess akilleshäl, vilket gör det svårt att integreras i elektroniska enheter.
"I halvledare, det finns en energiregion som kallas bandgapet där det inte finns några tillgängliga elektroniska tillstånd, ” Foa Torres, vid National University of Córdoba i Córdoba, Argentina, berättade PhysOrg.com . ”Man säger att bärardensiteten där är noll. Om du har din enhet ansluten mellan två elektroder och den inte har några tillgängliga tillstånd, då kan den elektriska strömmen genom den göras mycket liten. En halvledare med nollgap, även kallad en gapfri halvledare, är ett material där tätheten av elektroniska tillstånd försvinner vid en enda punkt. Detta är fallet för grafen, där pi- och pi*-banden berörs vid en enda punkt, den så kallade Dirac-punkten. I praktiken, de beter sig som att de inte har en lucka alls.
"Att sakna ett bandgap betyder att grafen inte kan "stängas av, ’” förklarade han. "Att ha "på" och "av"-strömmar kan koda information som 1:or och 0:or som är nödvändiga för beräkning och är avgörande för aktiva elektroniska enheter som switchar och transistorer. Detta är anledningen till att det att inte ha något bandgap är en av de största nackdelarna som hindrar många tillämpningar av detta enastående material."
I en ny studie, Foa Torres och hans medförfattare har tagit upp detta problem. Genom att analysera hur ett laserfält interagerar med elektroner i grafen, forskarna har förutspått att lysande av en mellaninfraröd laser på grafen kan skapa bandluckor i dess elektroniska struktur. Ytterligare, forskarna förutspår att bandluckan kan justeras genom att kontrollera laserpolariseringen. Som Foa Torres förklarade, nyckeln till hur polariserat ljus "öppnar upp" bandluckor i grafen involverar elektroner som interagerar med laserfältet.
"Föreställ dig en elektron som rör sig, säg från vänster till höger, in i ett område som är upplyst av laserfältet, " sa han. "Det som sedan händer är att elektronen interagerar med strålningen genom att absorbera eller sända ut fotoner. Denna interaktion leder till att elektronen reflekteras eller sprids tillbaka, som det skulle ha träffat en vägg:bandgapet. Till skillnad från vanliga bandluckor, den här produceras dynamiskt av lasern."
Genom att visa att ett laserfält kan användas för att ställa in den elektroniska strukturen hos grafen, studien har både grundläggande implikationer och tekniska tillämpningar.
"Samspelet mellan den speciella elektroniska strukturen hos grafen och lasern kan hjälpa till att inducera exotiska tillstånd av materia som topologiska isolatorer, material som är isolatorer i bulken men som visar robust ledning i ytan, " sa Foa Torres. "Å andra sidan, ur tillämpad synvinkel, Jag anser att dessa laserinducerade bandgap kan öppna en väg för en ny sort av optoelektroniska enheter, enheter som omvandlar optiska signaler till elektriska signaler."
För Foa Torres och hans medförfattare, nästa avgörande steg är experimentell verifiering.
"Experimentell verifiering av våra resultat är en av de viktigaste drivkrafterna för vårt projekt, " sa han. "I syfte att bana väg för experimentalister att kunna verifiera dem, vi har utfört en mycket finjustering av parametrar som laserfrekvens, amplitud, etc. Under de senaste månaderna har vi fått mycket värdefull feedback från experimentella grupper på toppnivå i USA och Spanien som är intresserade av vårt förslag. Som alltid, det finns säkert fortfarande några problem att lösa innan det blir verklighet men man bör gå steg för steg. Dörren är nu öppen, vi går precis in i en lovande terra incognita.”
Copyright 2011 PhysOrg.com.
Alla rättigheter förbehållna. Detta material får inte publiceras, utsända, omskrivs eller omdistribueras helt eller delvis utan uttryckligt skriftligt tillstånd från PhysOrg.com.