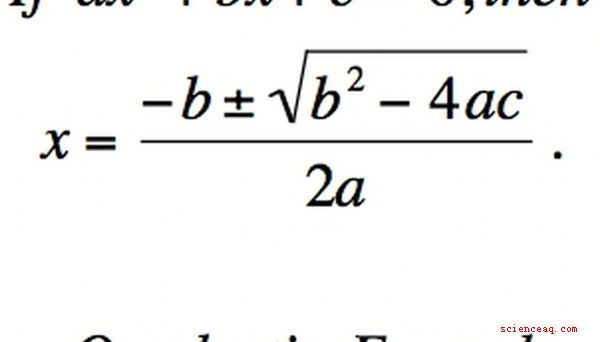
En polynomers factoring hänvisar till att hitta polynomier av lägre ordning (högsta exponent är lägre) som multipliceras tillsammans, ger det polynom som faktureras. Exempelvis kan x ^ 2 - 1 faktureras i x - 1 och x + 1. När dessa faktorer multipliceras, avbryts -1x och + 1x och lämnar x ^ 2 och 1.

Of Limited Power

Factoring är tyvärr inte ett kraftfullt verktyg, vilket begränsar användningen i vardagen och tekniska områden. Polynomier är starkt riggerade i grundskolan så att de kan beaktas. I vardagen är polynomier inte lika vänliga och kräver mer sofistikerade analysverktyg. Ett polynom så enkelt som x ^ 2 + 1 är inte faktorabelt utan att använda komplexa tal - det vill säga siffror som inkluderar i = √ (-1). Polynomier av ordning så låg som 3 kan vara orimligt svåra att faktor. Exempelvis är x ^ 3 - y ^ 3 faktorer till (x - y) (x ^ 2 + xy + y ^ 2), men det är inte längre utan att tillgripa komplexa tal.

br>

Andra ordningens polynomier - t.ex. x ^ 2 + 5x + 4 - är regelbundna fakturerad i algebra klasser, omkring åttonde eller nionde klass. Syftet med att factoring sådana funktioner är att sedan kunna lösa ekvationer av polynomier. Exempelvis är lösningen på x ^ 2 + 5x + 4 = 0 rötterna av x ^ 2 + 5x + 4, nämligen -1 och -4. Att kunna hitta rötterna till sådana polynomier är grundläggande för att lösa problem i vetenskapsklasserna under de följande 2 till 3 åren. Andra ordningens formler kommer regelbundet upp i sådana klasser, t.ex. i projektilproblem och syrabasbasjämviktsberäkningar.

Den kvadratiska formel

När du kommer upp med bättre verktyg för att ersätta factoring måste du komma ihåg vad syftet med factoring är i första hand: att lösa ekvationer. Den kvadratiska formeln är ett sätt att arbeta kring svårigheten att factoring vissa polynomier medan de fortfarande tjänar syftet att lösa en ekvation. För ekvationer av andra ordningens polynomier (dvs av formen ax ^ 2 + bx + c) används den kvadratiska formeln för att hitta polynomens rötter och därmed ekvationens lösning. Den kvadratiska formeln är x = [-b +/- √ (b ^ 2 - 4ac)] /[2a], där +/- betyder "plus eller minus". Observera att det inte finns något behov av att skriva (x - root1) (x - root2) = 0. I stället för factoring för att lösa ekvationen kan lösningen av formeln lösas direkt utan factoring som ett mellansteg, även om metoden är baserad på faktorisering.

Detta är inte att säga att factoring är dispensable. Om eleverna lärde sig den kvadratiska ekvationen för att lösa ekvationer av polynomier utan att lära sig factoring, skulle förståelsen för den kvadratiska ekvationen minskas.

Exempel på

Det här är inte att säga att faktorisering av polynomier aldrig görs utanför av algebra, fysik och kemi klasser. Handhållna ekonomiska räknemaskiner utför en ränteberäkning per dag med hjälp av en formel som är faktoriseringen av framtida betalningar med räntekomponenten backat ut (se diagram). I differentialekvationer (ekvationer för förändringshastigheter) utförs faktorisering av polynomerna av derivat (förändringshastigheter) för att lösa det som kallas "homogena ekvationer av godtycklig ordning". Ett annat exempel är i introduktionsberäkningen, i metoden för partiella fraktioner för att göra integrationen (lösning för området under en kurva) enklare.

Beräkningslösningar och användningen av bakgrundsundervisning

Dessa exempel är , naturligtvis, långt från vardagen. Och när factoring blir svårt, har vi miniräknare och datorer för att göra det tunga. Istället för att förvänta sig en en-till-en match mellan varje matematisk ämnesundervisning och vardagliga beräkningar, se på förberedelsen som ämnet ger för mer praktisk studie. Factoring bör uppskattas för vad det är: en steg till lärande metoder för att lösa mer realistiska ekvationer.