Vad betyder det för eleverna om de lär sig teknik kan svara på alla utmaningar?
Datorer har hjälpt matematisk forskning att accelerera i flera riktningar och ökat förekomsten av matematik i vardagen.
Teknikens roll i undervisning och inlärning av matematik är allt mer i mina tankar som matematiklärare som ser nya studenter anlända till Simon Fraser University (SFU) varje år. Både på SFU, och när jag besöker kanadensiska matematikklassrum som gästföreläsare, Jag tittar ut i rum fyllda med livfulla ungdomar omgivna av miniräknare, datorer och smarta telefoner.
Och det är okej. Som många matematiker, Jag har inte trängt mig tillbaka mot de nya tekniska vindar som inletts av modern tid. Men sådan teknik bör förbättra och utöka, istället för att ersätta, förmågan att tänka matematiskt.
Adieu geometri?
Nyligen, Jag träffade en ung person som var intresserad av matematik och datorer, men inte säker på vilken riktning han skulle vilja gå i. Jag erbjöd följande problem som användes av University of Oxford för att intervjua matematikkandidater:"Föreställ dig en stege lutad mot en vertikal vägg med fötterna på marken. stegen har målats i en annan färg på sidan, så att vi kan se det när vi tittar på stegen från sidan och framåt. Vilken form spårar det mittersta steget ut när stegen faller till golvet?"
Ett sätt att närma sig stegpusslet är att använda, på ett relativt enkelt sätt, euklidisk geometri, för att visa att svaret är en kvarts cirkel. Se nedan:
Istället för att dra på geometriska egenskaper, den unge mannen använde programmeringsspråket Python för att animera problemet och hitta den form som krävs. Han hade lärt sig Python på egen hand tidigare samma sommar. När jag frågade honom om kongruenta trianglar, den unge mannen såg förvirrad ut.
Situationer som denna gör mig rädd att om den inte används med vederbörlig försiktighet i klassrummen, teknik kan beröva eleverna att fullt ut utveckla sina räknefärdigheter och rumsliga färdigheter.
Ouppnåeliga problem
Det matematiker kallar "the computationally assisted approach" har gjort det möjligt för forskare att utforska och lösa matematiska problem som annars skulle vara oåtkomliga. Det datorstödda beviset på den berömda fyrfärgssatsen kommer att tänka på.
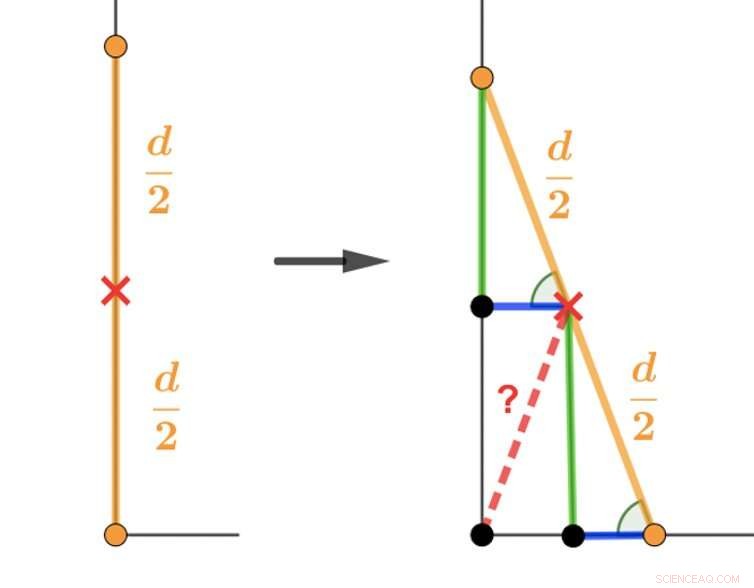
Euklidisk geometri kan användas för att lösa problemet som ges till University of Oxfords matematikkandidater. Kredit:Veselin, Författare tillhandahålls
Men vissa matematiska frågor har visat på begränsningar av befintlig teknik – och det faktum att vissa lösningar till stor del beror på mänsklig intuition, inspiration och intelligens. Ett sådant problem, känt som partiproblemet (ja, som i en middagsbjudning), är att hitta antalet gäster som skulle garantera att man alltid kan hitta sex personer som är gemensamma vänner eller sex personer som är gemensamma främlingar.
I matematiska termer, det här problemet handlar om att hitta vad som kallas "Ramsey-numret R(6, 6), " relaterat till en gren av matematiken som studerar vilka förutsättningar som måste finnas för att ett givet mönster ska uppstå.
Tro det eller ej, sedan 1930 har matematiker vetat att R(6, 6) existerar; sedan 1994 har vi vetat att detta nummer är mellan 102 och 165.
Inga framsteg sedan dess!
Experimentell matematik
Berömda kanadensiska matematiker och bröder Peter Borwein och Jonathan Borwein – som etablerade Center for Experimental and Constructive Mathematics 1993 vid SFU – var bland forskningspionjärer som bidrog till processen att anpassa matematik och ny teknologi.
Som föreslagits av Jonathan Borwein och matematikern David H. Bailey, experimentell matematik använder "en beräkningsunderstödd metod för matematisk forskning." De menade att experimentell matematik handlar om att använda datorer för att öka processer som har varit de grundläggande delarna av matematisk forskning i århundraden:
De hävdade också att datorer kunde hjälpa till med att utföra långa matematiska härledningar och bekräfta analytiskt härledda resultat.
Deras poäng var att datorer gör det möjligt för forskare att driva sina utforskningar till nya eller andra dimensioner.
Ny utforskning
Bailey och Borweins idéer kan användas för att beskriva samtida och framtida sätt att undervisa i matematik för att hjälpa elever att se på problem på nya sätt.
I min geometri-Python-anekdot, Jag kan ha utmanat eleven genom att observera att formen som erhålls av den Python-genererade animationen bara ser ut som en kvartscirkel (detta kan hänvisa till punkterna 1-3 och 5 i Bailey-Borwein-definitionen) och att ett fullständigt svar skulle kräva en analytiskt härlett resultat (punkt 6).
För att motivera utmaningen, Jag kanske också väljer att visa eleven ett till synes otrolig visuellt bevis, till exempel animationen som "visar" 64 =65.
Jag skulle kunna avsluta med att citera 1600-talets matematiker och filosof René Descartes, som beslutade:"... att aldrig acceptera något för sant som jag inte tydligt visste var sådant; det vill säga, försiktigt … undvik … fördomar, och att inte innehålla något mer i min bedömning än det som presenterades för mig så klart och tydligt att det utesluter all tvivel."
Experimentell matematik läroplaner
Forskare och utbildare har utvecklat läroplaner som är specialiserade på att lära barn och ungdomar hur man använder datorer för att förbättra och utöka sitt eget matematiska lärande och tänkande i kanadensiska gymnasieskolor. Till exempel, RabbitMath Curriculum Project, ledd av matematiker Peter Taylor från Queen's University och Chris Suurtamm från University of Ottawa, eller Callysto-projektet, försvaras av Pacific Institute for Mathematical Sciences (PIMS) och den Alberta-baserade ideella organisationen Cybera.
Utmaningen för matematiklärare kommer att handla om att i allt högre grad skapa och upprätthålla en sund balans i våra klassrum mellan kraften i rigorösa, formell matematik och datorkraften.
När jag tänker på framtiden, Jag är oroad över att de rigorösa och formella delarna av matematiken kan försvinna och lämnas utanför elevernas räckvidd.
För en student i en inte alltför avlägsen framtid, skulle, till exempel, talet pi blir ett rationellt tal – vilket betyder, skulle det vara lika med dess approximation som genereras av den mest kraftfulla datorn för tillfället?
Viktigast, vad kommer allt detta att betyda för eleverna och deras lärande av matematik som ett instrument för att bättre navigera i världen omkring dem?
Den här artikeln är återpublicerad från The Conversation under en Creative Commons-licens. Läs originalartikeln. 