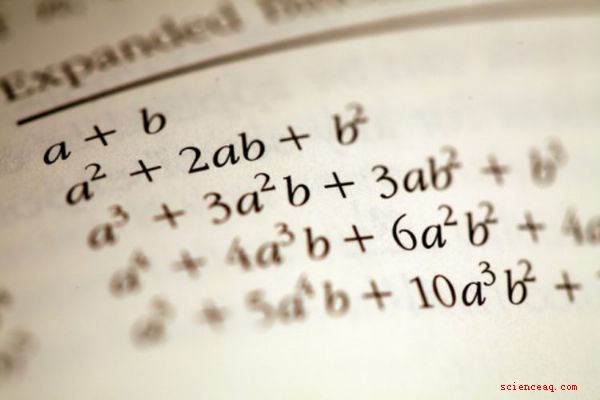
Multiplikation och tillägg är relaterade matematiska funktioner. Att lägga till samma antal flera gånger ger samma resultat som att multiplicera antalet med antalet gånger tillsatsen upprepades, så att 2 + 2 + 2 \u003d 2 x 3 \u003d 6. Detta förhållande illustreras ytterligare av likheter mellan associativet och multiplikationens kommutativa egenskaper och de associerande och kommutativa egenskaperna för tillsats. Dessa egenskaper hänför sig till att ordningen på siffrorna i ett tilläggs- eller multiplikationsnummer inte ändrar resultatet av ekvationen. Det är viktigt att notera att dessa egenskaper endast gäller tillägg och multiplikation och inte för subtraktion eller delning, där ändring av ordningen på siffrorna i ekvationen kommer att förändra resultatet.
Commutative Property of Multiplication

When multiplicera två siffror, omvänd ordning på siffrorna i ekvationen resulterar i samma produkt. Detta är känt som multiplikationens kommutativa egenskap och är ganska lik den associerande egenskapen för tillägg. Att till exempel multiplicera tre med sex är lika med sex gånger tre (3 x 6 \u003d 6 x 3 \u003d 18). Uttryckt i algebraiska termer är den kommutativa egenskapen axb \u003d bxa, eller helt enkelt ab \u003d ba.
Associativ egenskap för multiplikation.

Den associativa egenskapen för multiplikation kan ses som en förlängning av den kommutativa egenskapen för multiplikation och paralleller den associerande egenskapen av tillägg. När du multiplicerar mer än två siffror, ändrar du i vilken ordning numren multipliceras eller hur de grupperas resulterar i samma produkt. Till exempel (3 x 4) x 2 \u003d 12 x 2 \u003d 24. Att ändra multiplikationsordningen till 3 x (4 x 2) ger 3 x 8 \u003d 24. I algebraiska termer kan den associerande egenskapen beskrivas som (a + b) + c \u003d a + (b + c).
Kommutativ egenskap för tillägg |

Det kan vara till hjälp att komma ihåg de associativa och kommutativa egenskaperna för tillägg med hänvisning till multiplikationens associativa och kommutativa egenskaper. . Enligt den kommutativa egenskapen för tillägg resulterar två siffror som läggs samman i samma summa oavsett om de läggs framåt eller bakåt. Med andra ord, två plus sex är lika med åtta och sex plus två är också lika med åtta (2 + 6 \u003d 6 + 2 \u003d 8) och påminner om multiplikationens kommutativa egenskap. Återigen kan detta uttryckas algebraiskt som en + b \u003d b + a.
Associativ egenskap för tillägg |

I den associativa egenskapen för tillägg läggs ordningen till som mer än tre eller flera uppsättningar av nummer läggs samman ändrar inte summan av siffrorna. Således (1 + 2) + 3 \u003d 3 + 3 \u003d 6. Precis som i den associerande egenskapen för multiplikation ändrar inte ordningen resultatet eftersom 1 + (2 + 3) \u003d 1 + 5 \u003d 6. Algebraiskt, den associerande egenskapen för tillsats är (a + b) + c \u003d a + (b + c).