Tangenten är en av de tre grundläggande trigonometriska funktionerna, de andra två är sinus och kosinus. Dessa funktioner är viktiga för att studera trianglar och relaterar triangelns vinklar till dess sidor. Den enklaste definitionen av tangenten använder förhållandena på sidorna i en rätt triangel, och moderna metoder uttrycker denna funktion som summan av en oändlig serie. Tangenter kan beräknas direkt när längderna på sidorna i den högra triangeln är kända och kan också härledas från andra trigonometriska funktioner.

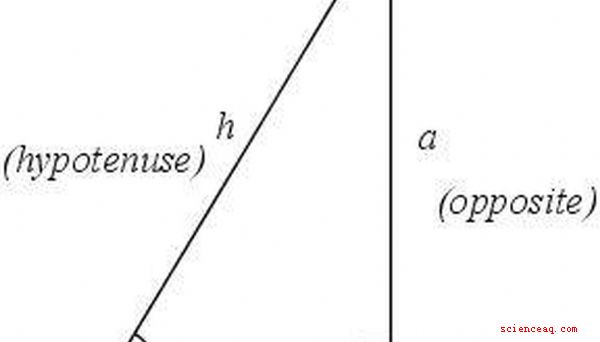
Identifiera och märka delarna av en rätt triangel. Rätt vinkel kommer att vara vid toppunkt C, och sidan motsatt den är hypotenusen h. Vinkeln &# x3B8; kommer att ligga vid toppunkt A, och återstående toppunkt kommer att vara B. Sidan intill vinkeln &# x3B8; kommer att vara sida b och sidans motsatta vinkel &# x3B8; kommer att vara sida a. De två sidorna av en triangel som inte är hypotenusen kallas benens triangel.


Definiera tangenten. En vinkelns tangent definieras som förhållandet mellan sidans längd mitt emot vinkeln och längden på sidan intill vinkeln. När det gäller triangeln i steg 1, solbränna &# x3B8; \u003d a /b.


Bestäm tangenten för en enkel höger triangel. Exempelvis är benen på en rät triangel med likbenet lika, så a /b \u003d solbränna &# x3B8; \u003d 1. Vinklarna är också lika så &# x3B8; \u003d 45 grader. Därför solbränna 45 grader \u003d 1.


Hämta tangenten från de andra trigonometriska funktionerna. Sedan sinus &# x3B8; \u003d a /h och kosinus &# x3B8; \u003d b /h, sedan sinus &# x3B8; /kosinus &# x3B8; \u003d (a /h) /(b /h) \u003d a /b \u003d solbränna &# x3B8 ;. \u003d sinus &# x3B8; /cosinus &# x3B8 ;.


Beräkna tangenten för valfri vinkel och önskad noggrannhet:


sin x \u003d x - x ^ 3/3! + x ^ 5/5! - x ^ 7/7! + ... kosinus x \u003d 1 - x ^ 2/2! + x ^ 4/4! - x ^ 6/6! + ... Så solbränna x \u003d (x - x ^ 3/3! + X ^ 5/5! - x ^ 7/7! + ...) /(1 - x ^ 2/2! + X ^ 4 /4! - x ^ 6/6! + ...)