Globala klimatmodeller, som Energy Exascale Earth System Model som utvecklats av U.S. Department of Energy, förlitar sig på många underliggande ekvationer som simulerar jordens naturliga processer. Dessa inkluderar vattnets kretslopp, koldioxidupptaget av land och vatten och hastigheten för issmältning.

Att verifiera och validera dessa ekvationer är avgörande för att skapa förtroende för klimatmodeller. Även om en viss diskrepans mellan modellförutsägelser och faktiska observationer är oundviklig, är målet att specifika konfigurationer av modellen ska konvergera till den korrekta lösningen i den hastighet som forskarna förväntar sig.

Kontinuerliga matematiska modeller måste genomgå en process som kallas diskretisering, som omvandlar dem till former som kan lösas numeriskt av datorer. Testfall kan hjälpa till med övergripande verifiering av en modell genom att extrahera delmängder av de diskretiserade ekvationerna och verifiera varje term.

Att mäta hastigheten med vilken de numeriska lösningarna i dessa testfall konvergerar mot de exakta lösningarna (vilket innebär att felen närmar sig noll) är guldstandardmetoden för modellverifiering. Konvergenshastigheter som överensstämmer med teoretiska förväntningar är den bästa garantin för att de diskretiserade ekvationerna är korrekt kodade.

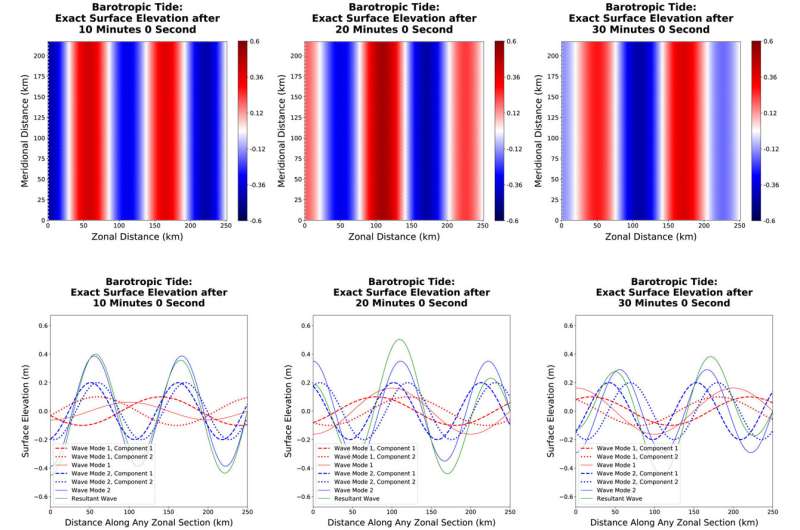
För beräkningseffektivitet delar havsmodeller vanligtvis upp sina styrande ekvationer i en 3D baroklinisk komponent som modellerar långsamma interna gravitationsvågor och havsströmmar och en 2D barotropisk komponent som modellerar snabba ytgravitationsvågor. Den barotropa komponenten antar formen av gruntvattenekvationer. Siddhartha Bishnu och kollegor presenterar en samling testfall fokuserade på dessa ekvationer. Forskningen publiceras i Journal of Advances in Modeling Earth Systems .

För att utveckla testfallen utgick forskarna från sin erfarenhet av att utveckla modellen för förutsägelse över skalor–hav (MPAS–Ocean), som används för att simulera havsaktivitet och studera hur den påverkas av antropogena klimatförändringar. Författarna noterar att deras testfall är avsedda att verifiera modellens noggrannhet (för att säkerställa att de diskretiserade modellekvationerna implementeras korrekt), snarare än att validera resultaten (för att säkerställa att modellförutsägelserna liknar observationer i den verkliga världen).

Forskarna granskade de teoretiska grunderna för ekvationerna i grunt vatten tillsammans med diskretiseringsmetoderna, gav en översikt över testfallen för att säkerställa reproducerbarhet och visade att konvergenshastigheterna matchar de förväntade förutsägelserna.

Dessa testfall kommer att göra det möjligt för andra forskare att bedöma sina modellers komponenter utan att behöva överdriven beräkningskraft, skriver författarna. Dessutom kan testfallen vara användbara för bredare vätskedynamikproblem och fungera som instruktionsverktyg för att studera och utveckla havsmodeller.

Mer information: Siddhartha Bishnu et al, A Verification Suite of Test Cases for the Barotropic Solver of Ocean Models, Journal of Advances in Modeling Earth Systems (2024). DOI:10.1029/2022MS003545

Tillhandahålls av American Geophysical Union

Denna berättelse är återpublicerad med tillstånd av Eos, värd av American Geophysical Union. Läs originalberättelsen här.