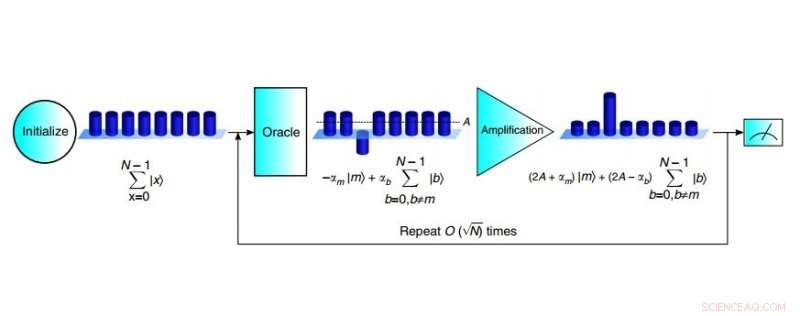
De tre stadierna i 3-qubit Grover-sökalgoritmen:initialisering, orakel, och förstärkning. Upphovsman:C. Figgatt et al. Publicerad i Naturkommunikation
Söker stort, oordnade databaser för ett önskat objekt är en tidskrävande uppgift för klassiska datorer, men kvantdatorer förväntas utföra dessa sökningar mycket snabbare. Tidigare forskning har visat att Grovers sökalgoritm, föreslog 1996, är en optimal kvantsökningsalgoritm, vilket innebär att ingen annan kvantalgoritm kan söka snabbare. Dock, att implementera Grovers algoritm på ett kvantsystem har varit utmanande.
Nu i en ny studie, forskare har implementerat Grovers algoritm med fångade atomjoner. Algoritmen använder tre qubits, som motsvarar en databas med 8 (2 3 ) objekt. När den används för att söka i databasen efter ett eller två objekt, Grover -algoritmens framgångssannolikheter var - som förväntat - betydligt högre än de bästa teoretiska framgångssannolikheterna för klassiska datorer.
Forskarna, Caroline Figgatt et al., vid University of Maryland och National Science Foundation, har publicerat en uppsats om sina resultat i ett nyligen utgåva av Naturkommunikation .
"Detta arbete är det första genomförandet av en 3-qubit Grover-sökalgoritm i ett skalbart kvantdatasystem, "Berättade Figgatt Phys.org . "Dessutom, detta är den första implementeringen av algoritmen med hjälp av booleska orakler, som kan jämföras direkt med en klassisk sökning. "
Det klassiska tillvägagångssättet för att söka i en databas är enkelt. I grund och botten, algoritmen gissar slumpmässigt ett objekt, eller "lösning". Så, till exempel, för en enda sök iteration på en databas med 8 objekt, en klassisk algoritm gör en slumpmässig fråga och, om det misslyckas, det gör en andra slumpmässig gissning - totalt sett gissa 2 av 8 artiklar, vilket resulterar i 25% framgång.
Grovers algoritm, å andra sidan, initialiserar först systemet i en kvantöverlagring av alla åtta tillstånd, och använder sedan en kvantfunktion som kallas ett orakel för att markera rätt lösning. Som ett resultat av dessa kvantstrategier, för en enda sök iteration på en 8-objekt databas, den teoretiska framgångsgraden ökar till 78%. Med en högre framgång kommer snabbare söktider, eftersom det i genomsnitt behövs färre frågor för att komma fram till rätt svar.
Vid implementeringen av Grovers algoritm som rapporteras här, framgångsgraden var lägre än det teoretiska värdet - ungefär 39% eller 44%, beroende på vilket orakel som används - men fortfarande markant högre än den klassiska framgångsgraden.
Forskarna testade också Grovers algoritm på databaser som har två korrekta lösningar, i så fall är de teoretiska framgångarna 47% och 100% för klassiska och kvantdatorer, respektive. Genomförandet som visats här uppnådde framgångsgrader på 68% och 75% för de två orakeltyperna - igen, bättre än det högsta teoretiska värdet för klassiska datorer.
Forskarna förväntar sig att i framtiden, denna implementering av Grovers algoritm kan skalas upp till större databaser. När databasens storlek ökar, kvantfördelen jämfört med klassiska datorer blir ännu större, det är där framtida applikationer kommer att gynnas.
"Går vidare, vi planerar att fortsätta utveckla system med förbättrad kontroll över fler qubits, "Sade Figgatt.
© 2018 Phys.org