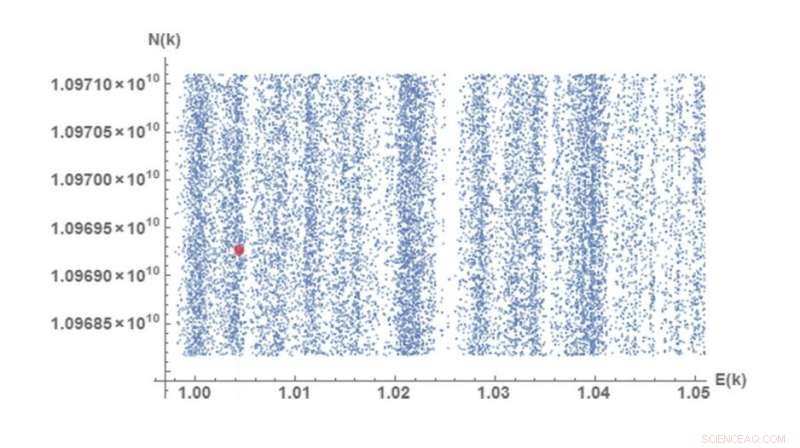
Denna diagram av värden i faktoriseringsensemblen på 10, 000 visar att värdena korrelerar med bandspektrumet för ett kvantsystem. Den röda pricken markerar ett exempel:punkten N =10, 969, 262, 131 =47, 297 x 231, 923, E =1.00441815 (där Ek är en funktion som beskrivs i tidningen). Upphovsman:Rosales och Martin. © 2018 American Physical Society
Att klassificera mycket stora siffror i sina främsta "byggstenar" är extremt svårt för klassiska datorer, och denna svårighet ligger till grund för säkerheten för många kryptografiska algoritmer. Även om det är lätt att faktorera talet 20 som produkten av primtalen 2 x 2 x 5, till exempel, factoring större antal blir exponentiellt svårare när du använder klassiska factoring algoritmer.
I en ny artikel publicerad i Fysisk granskning A , fysikerna Jose Luis Rosales och Vicente Martin har utvecklat en metod som kan göra det mycket lättare att faktorera mycket stora tal som är kända för att ha exakt två primära faktorer. Den nya metoden bestämmer sannolikheten för att ett primtal är en av de två primfaktorerna för ett givet tal. Efter att ha bestämt dessa odds, de mest troliga primfaktorkandidaterna kan testas först, så att de viktigaste faktorerna kan identifieras mycket snabbare än tidigare.
"Teorin visar inte bara var primtalen finns, men också sannolikheten för att ett primtal är en faktor för ett givet tal, "Berättade Rosales Phys.org . "Självklart, detta har konsekvenser för kryptografi eftersom [kryptosystemet] RSA ignorerar denna regelbundenhet. "
En av de intressanta sakerna med den nya metoden är att den inte använder någon form av dator, antingen klassisk eller kvant. Istället innebär det ett fysiskt kvantsystem - en "kvantsimulator" - att, när kodad med siffran till faktor, uppvisar en sannolikhetsfördelning av energivärden som är ekvivalent med sannolikhetsfördelningen för primfaktorkandidaterna för det kodade talet.
"Vårt mål är att utveckla en ny kvantteori om faktoriseringsproblemet med hjälp av en kvantsimulator, "Rosales sa." Vår metod har upptäckt en egenskap utan klassisk analogi i talteori. Varje par primtal som löser problemet ordnar om sig själva för att bilda ett vanligt mönster:bandspektrumet för kvantsimulatorn. "
Den allmänna idén bakom kvantsimulatorn är något som kallas "faktoriseringsensemblen, "som forskarna introducerade tidigare. Det bygger på tanken att primtalen är ordnade från minst till störst (t.ex. 2 är den första prime, 3 är den andra prime, och 101 är den 26 th främsta). Det är också möjligt att ta kvadratroten på valfritt tal, och jämför sedan resultatet med närmaste primtal. Till exempel, kvadratroten på 27 är lite mer än 5, som är den tredje primtalen. Genom definitionen av en faktoriseringsensemble, detta betyder att 27 tillhör faktoriseringsensemblen 3.
Fysikerna visade sedan att de kunde omvandla faktoriseringsensemblefunktionen till en funktion från kvantfysik (den inverterade harmoniska-oscillatorfunktionen). Efter många fler steg, de visade så småningom att det förutspådda energispektrumet för ett kvantsystem motsvarar fördelningen av primtal i faktoriseringsensemblen för ett tal. Från denna information, forskarna kan bestämma sannolikheten för att ett primtal är en faktor för det numret. För att testa giltigheten av deras metod, fysikerna testade vissa siffror och jämförde sina resultat med de faktiska fördelningarna som erhölls med hjälp av primtalstabeller, och hittade mycket liknande fördelningar.
Fysikerna visade teoretiskt att den föreslagna kvantsimulatorn kan faktorera tal som är många storleksordningar större än de som har räknats med kvantdatorer. I deras papper, de rapporterar resultaten av att använda sin metod för att bestämma sannolikhetsfördelningen av primfaktorerna för ett tal med 24 siffror. Ytterligare, metoden gör detta med mycket färre resurser än vad klassiska factoringalgoritmer kräver.
"I kvantteori, den algoritmiska komplexiteten är bara polynom med antalet bitar i talet som ska faktoriseras, "Sa Rosales." Faktum är att våra första resultat verkar bekräfta att simulatorn endast kräver (log√N) 3 kvanttillstånd för att återge sitt spektrum av energier, ett mycket uppmuntrande resultat. "
En sista intressepunkt är att den nya metoden har starka kopplingar till Riemann -hypotesen, som, om sant, skulle föreslå att primtalen fördelas på ett förutsägbart sätt-på samma sätt som fördelningen av nollorna i Riemann-zeta-funktionen. Att bevisa (eller motbevisa) Riemann -hypotesen är ett av de största olösta problemen inom matematik, och ett av Clay Mathematics Institute:s Millenium Prize Problem.
"Primtalen bör bete sig som kvantnummer om Hilbert-Polyas gissning gäller, "Rosales sa, med hänvisning till det mångåriga tillvägagångssättet för att bevisa Riemann-hypotesen.
Går framåt, forskarna arbetar för närvarande med experimentell implementering av kvantsimulatorn genom att använda två intrasslade partiklar i en Penning -fälla.
"Den fullständiga kvantbehandlingen av simulatorn skulle kräva kvantoptisk analys av fotons interaktioner med två (eller flera) intrasslade joner i en Penning -fälla, "Sade Rosales." Denna del av programmet är ännu under utveckling. Syftet är att bygga en kvantfaktoringssimulator experimentellt. Om det genomförs framgångsrikt, nummer många storleksordningar större än de som är tillgängliga för dess kvantbehandling med Shors algoritm kommer att faktoriseras och, som en biprodukt, gissningen Hilbert-Polya kommer att testas experimentellt. "
© 2018 Phys.org