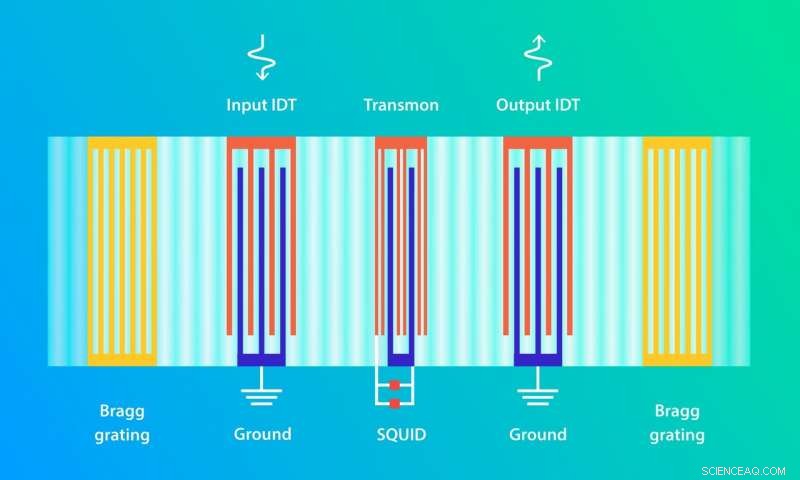
Figur 1. Schematisk över chipet. Resonatorn är en Fabry-Perot-hålighet som bildas av två Bragg-galler, var och en består av 200 parallella ränder (visas i gult) åtskilda med hälften av den akustiska våglängden. Våglängden är lika med 0,98 mikrometer, eller 980 nanometer. Det finns två interdigital transducer (IDT) portar - en mottagare och en sändare - och en qubit (transmon) inuti resonatorn. SQUID är den del av transmonen som är känslig för svaga magnetfält. Upphovsman:Elena Khavina/MIPT
Forskare från Ryssland och Storbritannien har visat ett artificiellt kvantsystem där en kvantbit interagerar med en akustisk resonator i kvantregimen. Detta gör att kvantoptikprinciper kan tillämpas vid studier av akustiska vågor och möjliggör ett alternativt tillvägagångssätt för kvantdatordesign baserad på akustik. Det kan också göra kvantdatorer mer stabila och kompakta. Papperet som rapporterar resultaten publicerades i Fysiska granskningsbrev .
"Vi är de första som demonstrerar en interaktion mellan en qubit och en ytvågsresonator i kvantregimen. Tidigare, resonatorer av detta slag studerades, men utan en qubit. Likaså, qubits med ytakustiska vågor studerades, men det var rinnande vågor, utan resonator. Kvantregimen demonstrerades på bulkresonatorer, men det här gick inte långt, kanske på grund av svårigheter att tillverka. Vi använde en plan struktur tillverkad med befintlig teknik, "säger Aleksey Bolgar, forskare vid MIPT:s Artificial Quantum Systems Lab, där studien genomfördes.
Forskarna studerade interaktionen mellan en supraledande qubit, en transmon, med akustiska ytvågor i en resonator (figur 1). Transmonen beter sig som en artificiell atom - det vill säga den har ett antal energinivåer (figur 2) och genomgår övergångar mellan dem. Den konventionella mikrovågsmetoden är att ha ett chip som håller både qubit och en mikrovågsresonator som stödjer och förstärker vågen. I denna inställning, qubit kan interagera med resonatorn antingen genom att absorbera en foton från den och gå in i ett upphetsat tillstånd eller genom att avge en foton till den och återgå till grundtillståndet, förutsatt att fotonfrekvensen motsvarar qubitens övergångsfrekvens. Resonatorns resonansfrekvens varierar beroende på qubitens tillstånd. Därför, genom att ändra resonatoregenskaper, det är möjligt att läsa information från qubit.
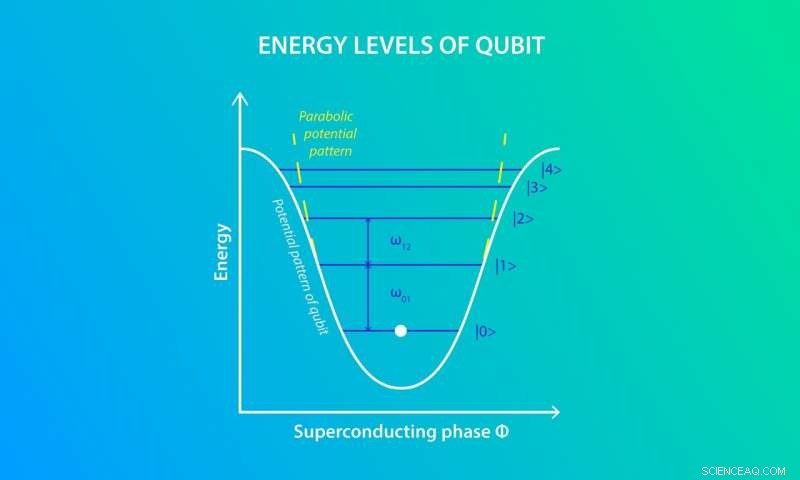
Figur 2. En transmons energispektrum liknar en atom. Övergångsfrekvensen mellan de två första energinivåerna är ω₀₁. Kredit:Elena Khavina/MIPT
Ett alternativt tillvägagångssätt har nyligen framkommit. Istället mikrovågsstrålning (fotoner), den använder mekaniska excitationer, eller fononer, i form av akustiska vågor. Detta kvantakustiska tillvägagångssätt har utvecklats i mycket mindre utsträckning, jämfört med sin mikrovågsmotsvarighet, men det har ett antal fördelar.
Eftersom akustiska vågor sprider sig 100, 000 gånger långsammare än ljus, deras våglängd är därför kortare. Storleken på en resonator måste "passa" den använda våglängden. I ett mikrovågskvantsystem, våglängden är i bästa fall cirka 1 centimeter. Det betyder att resonatorn måste vara ganska stor, men ju större den är, ju fler defekter den har, eftersom de oundvikligen finns på chipets yta. På grund av dessa defekter, livslängden för ett qubit-tillstånd är kort, försämra storskaliga kvantberäkningar och försvåra skapandet av kvantdatorer. Från och med nu, världsrekordet för den längsta livslängden är runt 100 mikrosekunder, eller en tiotusendels sekund. Under det akustiska tillvägagångssättet, våglängden är ungefär 1 mikrometer, så det är möjligt att montera högkvalitativa resonatorer som bara mäter 300 mikrometer på chipet.
Ett annat problem med mikrovågor är att de långa våglängderna gör det omöjligt att lägga två qubits i en resonator för att möjliggöra interaktion vid olika frekvenser. Som ett resultat, en separat resonator behövs för varje qubit (se figur 3). I det akustiska tillvägagångssättet, en mekanisk resonator kan rymma flera qubits med något olika övergångsfrekvenser. Detta innebär att ett kvantchip baserat på ljudvågor skulle vara mycket mindre än de som är tillgängliga nu. Dessutom, akustodynamik kan lösa frågan om kvantsystemets känslighet för elektromagnetiskt brus.
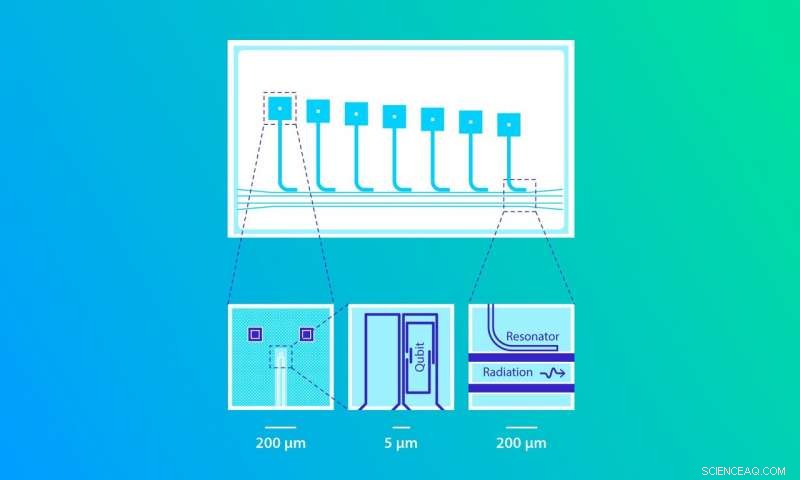
Figur 3. Mikrovågsflis. Var och en av de sju kvadratiska regionerna i den översta bilden innehåller en qubit. De L-formade linjerna på den översta bilden är mikrovågsresonatorer, var och en har en distinkt resonansfrekvens. En mikrometer (1 μm) är en miljonedel av en meter. Upphovsman:Elena Khavina/MIPT
Författarna till tidningen använde en resonator för ytakustiska vågor. Dessa påminner något om havsvågor men sprider sig i fasta ämnen. Figur 4 visar chipet som skapades i studien. En aluminiumkrets deponeras på ett piezoelektriskt substrat av kvarts. Kretsen består av en transmon, en resonator, och två interdigitalomvandlare. De två givarna fungerar som sändare och mottagare. Mellan dem, det finns ett piezoelektriskt lager av ett material som omvandlar mekanisk spänning till elektricitet och vice versa. En akustisk ytvåg som genereras på det piezoelektriska materialet fångas upp mellan de två Bragg-gittren i resonatorn. Qubiten, eller transmon, som finns i resonatorn har två energinivåer, och qubit -kapacitansen implementeras som interdigitalomvandlare. Syftet med studien var att visa att qubit kan interagera med resonatorn, bli upphetsad och avslappnad som ett kvantsystem skulle. Mätningarna gjordes i en kryostat under temperaturer i tiotals millikelvin.
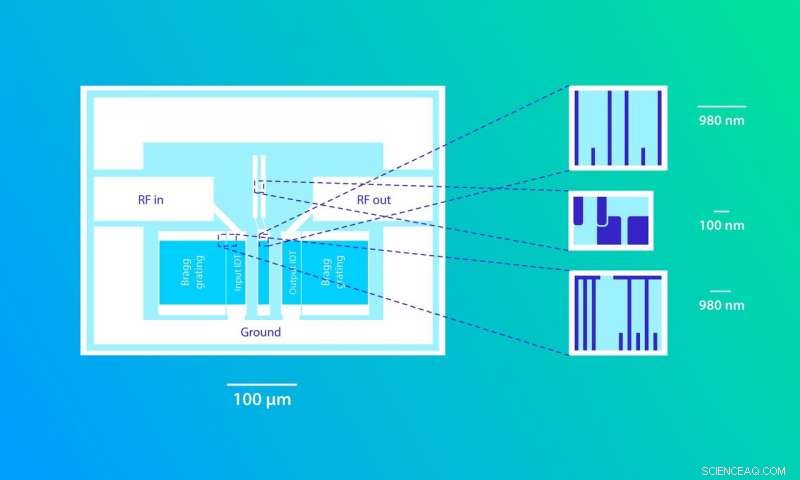
Figur 4. Akustiskt chip. Storleken på hela systemet är jämförbar med storleken på det förstorade kvadratområdet i figur 3. En nanometer (1 nm) är en miljarddels meter och en tusendels mikrometer (1 μm). RF står för radiofrekvens. Upphovsman:Elena Khavina/MIPT
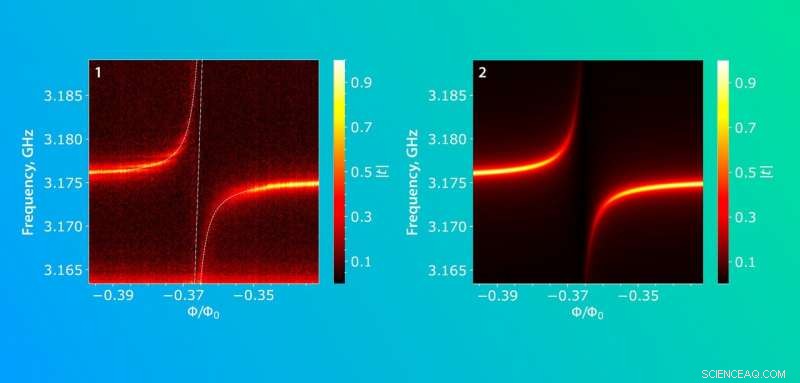
Ett kännetecken för kvantregimen är den så kallade undvikna korsningen av energinivåer (figur 5). Övergångsfrekvensen för qubiten kan ställas in via ett externt magnetfält - för att möjliggöra detta, transmon är utrustad med en SQUID magnetometer. Om resonatorns frekvens sammanfaller med qubit -övergångsfrekvensen, energisplittring observeras i energispektrumet för qubiten - det vill säga ett magnetiskt flödesvärde motsvarar två karakteristiska övergångsfrekvenser. Forskarna observerade detta fenomen i sitt chip och visade att transmon och akustisk resonator interagerar i kvantregimen.
Det grundläggande målet med denna forskning är att visa att fenomen och effekter av kvantoptik gäller även akustik. Dessutom, det ger ett alternativt sätt att bygga en kvantdator. Trots att mikrovågsbaserade gränssnitt uppnår ett imponerande antal 50 qubit, vilket betyder att kvantakustiken fortfarande har en lång väg att gå, det senare tillvägagångssättet har många fördelar som kan komma väl till pass i framtiden.
Figur 5. Signalens intensitet som överförs genom resonatorn är färgkodad som en funktion av signalfrekvensen och det magnetiska flödet. De experimentella mätningarna visas i (a) bredvid de teoretiska förutsägelserna (b) baserat på lösningen av kvantmodellekvation. Upphovsman:Elena Khavina/MIPT