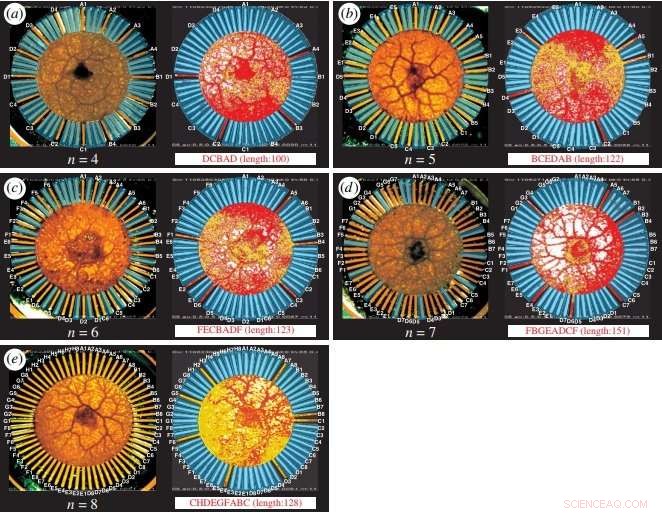
TSP-lösningar erhållna av det amöba-baserade datorsystemet för 4, 5, 6, 7, och 8 städer. Kredit:Zhu et al. ©2018 Royal Society Open Science
Forskare har visat att en amöba - en encellig organism som mestadels består av gelatinös protoplasma - har unika datorförmågor som en dag kan erbjuda ett konkurrenskraftigt alternativ till metoderna som används av konventionella datorer.
Forskarna, leds av Masashi Aono vid Keio University, tilldelas en amöba för att lösa problemet med resande säljare (TSP). TSP är ett optimeringsproblem där målet är att hitta den kortaste vägen mellan flera städer, så att varje stad besöks exakt en gång, och start- och slutpunkterna är desamma.
Problemet är NP-hårt, vilket innebär att när antalet städer ökar, tiden det tar för en dator att lösa det växer exponentiellt. Komplexiteten beror på det stora antalet möjliga lösningar. Till exempel, för fyra städer, det finns bara tre möjliga vägar. Men för åtta städer, antalet möjliga rutter ökar till 2520.
I den nya studien, forskarna fann att en amöba kan hitta rimliga (nästan optimala) lösningar på TSP på en tid som bara växer linjärt när antalet städer ökar från fyra till åtta. Även om konventionella datorer också kan hitta ungefärliga lösningar i linjär tid, amöbans tillvägagångssätt är helt annorlunda än traditionella algoritmer. Som forskarna förklarar, amöban utforskar lösningsutrymmet genom att kontinuerligt omfördela gelén i dess amorfa kropp med konstant hastighet, samt genom att bearbeta optisk feedback parallellt istället för seriellt.
Även om en konventionell dator fortfarande kan lösa TSP mycket snabbare än en amöba, speciellt för små problemstorlekar, de nya resultaten är spännande och kan leda till utvecklingen av nya analoga datorer som härleder ungefärliga lösningar på beräkningsmässigt komplexa problem av mycket större storlekar i linjär tid.
Hur det fungerar
Den speciella typ av amöba som forskarna använde var en plasmodium eller "äkta slemmögel, " som väger cirka 12 mg och konsumerar havreflingor. Denna amöba deformerar kontinuerligt sin amorfa kropp genom att upprepade gånger tillföra och dra ut gel med en hastighet av cirka 1 mm/sekund för att skapa pseudopodliknande bihang.
I deras experiment, forskarna placerade amöban i mitten av ett stjärnchip, som är en rund platta med 64 smala kanaler som skjuter utåt, och placerade sedan chipet ovanpå en agarplatta. Amöban är instängd i chipet, men kan fortfarande flytta in i de 64 kanalerna.
För att maximera upptaget av näringsämnen, amöban försöker expandera inuti chipet för att komma i kontakt med så mycket agar som möjligt. Dock, amöban gillar inte ljus. Eftersom varje kanal selektivt kan belysas med ljus, det är möjligt att tvinga amöban att dra sig tillbaka från de upplysta kanalerna.
För att modellera TSP, varje kanal i stjärnchipet representerar en ordnad stad i säljarens rutt. Till exempel, i fallet med fyra städer märkta A-D, om amöban upptar kanalerna A4, B2, C1, och D3, då är motsvarande lösning till TSP:n C, B, D, A, C.
För att styra amöban mot en optimal eller nästan optimal lösning, nyckeln ligger i att kontrollera ljuset. Att göra detta, forskarna använder en neural nätverksmodell där systemet var sjätte sekund uppdaterar vilka kanaler som är upplysta. Modellen innehåller information om avståndet mellan varje par av städer, samt feedback från amöbans nuvarande position i kanalerna.
Modellen säkerställer att amöban hittar en giltig lösning på TSP på några sätt. Till exempel, när amöban har ockuperat en viss del av en viss kanal, säg A3, sedan kanal A1, A2, och alla andra "A"-kanaler är upplysta för att förhindra att stad A besöks två gånger. Också, B3, C3, D3, och alla andra "3" kanaler är upplysta för att förbjuda samtidiga besök i flera städer.
Modellen tar hänsyn till avstånden mellan städer genom att göra det lättare att belysa kanaler som representerar städer med längre avstånd än med kortare avstånd. Till exempel, säg att amöban ockuperar kanal B2, och har börjat tränga in i kanalerna C3 och D3 i lika stora mängder, och avståndet mellan städerna B och C är 100 medan avståndet mellan städerna B och D är 50. Det längre avståndet mellan B och C gör att systemet så småningom lyser upp kanal C3, får amöban att dra sig tillbaka från den kanalen men låter den fortsätta att röra sig in i D3.
Övergripande, modellering av TSP med en amöba utnyttjar amöbans naturliga tendens att söka efter en stabil jämvikt. Eftersom kanaler som representerar kortare rutter är mindre benägna att vara upplysta, amöban kan spridas ut i dessa kanaler och fortsätta att utforska andra icke-upplysta kanaler för att maximera sin yta på agarplattan.
Forskarna utvecklade också en datorsimulering som heter AmoebaTSP som efterliknar några av huvuddragen i hur amöban löser problemet, inklusive den kontinuerliga rörelsen av gel då den tillförs med konstant hastighet och dras ut från olika kanaler.
"I vårt stellate chip för att lösa n -stad TSP, den totala arean av amöbans kropp blir n när amöban äntligen hittar en ungefärlig lösning, " berättade Aono Phys.org . "Det verkar finnas en "lag" att amöban levererar sin gelatinösa resurs för att expandera i de icke-upplysta kanalerna med en konstant hastighet, säga, x . Denna lag skulle behållas även när vissa resurser studsar tillbaka från upplysta kanaler. Sedan den tid som krävs för att utöka kroppsytan n att representera lösningen blir n / x . Denna mekanism skulle vara ursprunget till den linjära tiden, och det reproducerades av vår datorsimuleringsmodell.
"Men ändå, mekanismen genom vilken hur amöban upprätthåller kvaliteten på den ungefärliga lösningen, det är, den korta sträckan, förblir ett mysterium. Det verkar som om rumsligt och tidsmässigt korrelerade rörelser av de grenade delarna av amöban som ligger vid avlägsna kanaler är nyckeln. Var och en av dessa grenar oscillerar sin volym med något tidsmässigt "minne" på upplysta upplevelser. Grupper av grenarna utför synkronisering och avsynkronisering för att dela information även om de är rumsligt avlägsna."
I framtiden, forskarna planerar att ytterligare förbättra amöbans beräkningsförmåga.
"Vi kommer att undersöka ytterligare hur denna komplexa spatiotemporala oscillerande dynamik förbättrar beräkningsprestandan för att hitta lösningar av högre kvalitet på kortare tid, " sa medförfattaren Song-Ju Kim vid Keio University. "Om det kunde klargöras, kunskapen kommer att bidra till att skapa nya analoga datorer som utnyttjar den spatiotemporala dynamiken hos elektrisk ström i dess krets.
"Självklart, kör några andra algoritmer på traditionella digitala datorer för linjär tid, vi kan härleda ungefärliga lösningar till TSP. Å andra sidan, när vi kör våra simuleringsmodeller (AmoebaTSP eller dess utvecklade versioner) på de traditionella datorerna som vi gjorde i denna studie, den analoga och parallella spatiotemporala dynamiken kräver olinjär tid för att simulera dem som digitala och seriella processer. Så vi försöker få lösningar av mycket högre kvalitet än de som härrör från de traditionella genom att köra våra modeller på de analoga datorerna under linjär tid eller kortare."
Forskarna förväntar sig också att genom att tillverka ett större chip, amöban kommer att kunna lösa TSP-problem med hundratals städer, även om detta skulle kräva tiotusentals kanaler.
© 2018 Science X Network