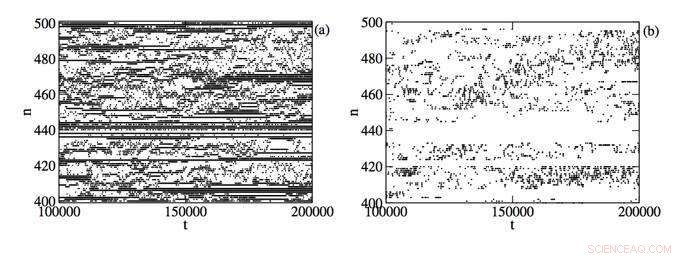
Figur 1:Spatiotemporal utveckling av en del av Josephson -kedjan. Vänster plot:tidsutveckling av en del av systemet med supraledande korn. Svartvita punkter motsvarar överskott och frånvaro av energi på varje spannmål. Rätt plot:tidsutveckling över samma del av systemet med svarta punkter som representerar kaotiska fläckar, där tre närliggande korn ger resonans. Kredit:Institute for Basic Science
Upptäckten av supraledning och dess experimentella förverkligande är två av de viktigaste framstegen inom fysik och teknik under det senaste århundradet. Ändå, deras statistiska och dynamiska egenskaper har ännu inte förståtts fullt ut. Ett team av forskare vid Center for Theoretical Physics of Complex Systems, inom Institute for Basic Science (IBS, Sydkorea), har modellerat energibeteendet för kaotiska nätverk av supraledande element (korn), åtskilda av icke-supraledande korsningar, och upptäckte länge några oväntade statistiska egenskaper, men ändå begränsade tidsskalor. Deras resultat publiceras i Fysiska granskningsbrev .
Ett antal banbrytande upptäckter inom statistisk mekanik uppstod från att ifrågasätta tillämpningen av abstrakta kärnbegrepp på fysiska system och experimentella enheter. Ett anmärkningsvärt exempel är den ergodiska hypotesen, som antar att med tiden, ett system besöker nästan alla tillgängliga mikrostater i fasutrymmet, och att det oändliga tidsgenomsnittet för en mätbar mängd av systemet matchar med dess fasutrymme -medelvärde. Kortfattat, detta är anledningen till att is smälter i en kruka med vatten. Och det kommer att göra det snabbare om vattnet är varmare. Forskare har funderat ut sätt att verifiera giltigheten eller misslyckandet av den ergodiska hypotesen baserat på mätningar med begränsad tid.
Under ledning av Sergej Flach, IBS -forskarna utvecklade en effektiv metod för att extrahera exakta uppskattningar av tidsskalorna för ergodicitet (myntad ergodiseringstid). Denna metod har härmed framgångsrikt tillämpats på klassiska nätverk av supraledande korn som är svagt kopplade av Josephson -korsningar.
Teamet fann att i dessa nätverk, ergodiseringstidsskalan blir snabbt enorm, även om det förblir ändligt, vid höjning av systemtemperaturen. Istället, tidsskalorna som är nödvändiga för att kaotik ska utvecklas förblir praktiskt taget oförändrade med avseende på ergodiseringen. Detta är mycket förvånande, eftersom ergodicitet är oupplösligt knuten till kaos, och deras respektive tidsskalor måste också vara strikt relaterade. När det gäller isen, det betyder att ju varmare vattnet blir, desto längre tid tar det innan isbitarna smälter. IBS -forskare visade numeriskt att högre temperaturfluktuationer starkt hindrar deras egen slingring genom systemet. Således, en långsammare och långsammare process försenar ergodiseringen av systemet drastiskt. Teamet har märkt denna upptäckt som "dynamiskt glas".
"När temperaturen höjs, våra studier avslöjade uppkomsten av roaming kaotiska fläckar bland frysta och till synes inerta regioner. Namnet dynamiskt glas följer av just denna fragmentering, som ordet "dynamisk" antyder den snabba utvecklingen av kaos, medan ordet "glas" pekar på fenomen som kräver en extremt lång men begränsad tidsskala för att inträffa, "förklarar Carlo Danieli, en medlem i teamet.
Förståelsen av mekanismen och de nödvändiga tidsskalorna för att ergodicitet och kaotik ska utvecklas är själva kärnan i ett stort antal senaste framsteg inom kondenserad fysik. Teamet förväntar sig att detta banar väg för att bedöma flera olösta problem i många kroppssystem, från avvikande värmeledningsförmåga till termalisering.
Forskarna förväntar sig också att det observerade dynamiska glaset är en generisk egenskap hos nätverk av supraledande korn via Josephson -koppling oavsett deras rymddimensionalitet. Vidare, det gissas att en bred uppsättning svagt icke-integrerbara system med många kroppar förvandlas till dynamiska glasögon när de närmar sig specifika temperaturregimer. En lika charmig och utmanande uppgift är teamets strävan att demonstrera förekomsten av ett dynamiskt glas i kvantmångkroppssystem, och upprätta sitt samband med fenomen med många lokaliseringsfunktioner.
Flach säger, "Vi förväntar oss att dessa fynd öppnar en ny plats för att bedöma och förstå fenomen relaterade till lokalisering och glasighet i många kroppar i ett stort antal svagt icke-integrerbara system med många kroppar."