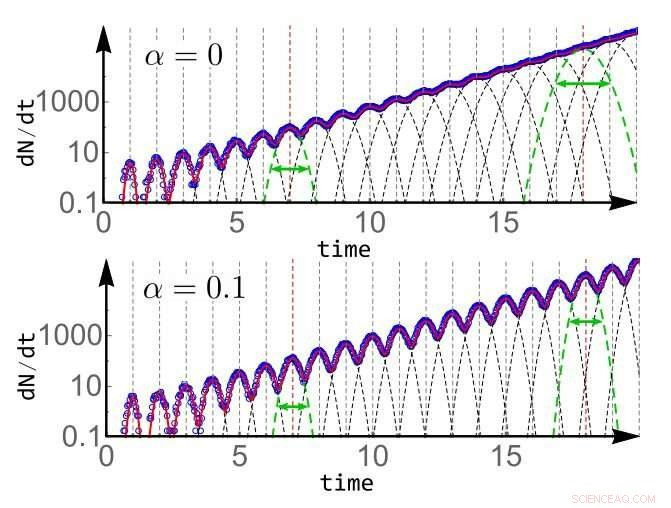
Log-skala plot av det förväntade värdet av förändringstakten för antalet celler i en population som börjar med en enda cell, beräknas analytiskt (röd solid kurva) och jämförs med simulering (blå cirklar). Ändringstakten för antalet celler kan skrivas som summan av delningshastigheterna (paraboliska streckade linjer) för alla generationer. (Överst) I avsaknad av cellstorlekskontroll, α =0, fördelningen av divisionstider för högre generationer blir bredare och börjar överlappa varandra, dämpa svängningarna i tillväxttakten. (Nederst) I närvaro av även en liten cellstorlekskontroll, α =0,1, fördelningen av successiva uppdelningstider närmar sig snabbt en steady state -fördelning med en ändlig variation som leder till att svängningar i befolkningens tillväxt kvarstår. Fördelningen av tidpunkten för 7:e och 18:e generationen belyses i båda fallen för jämförelse. Kredit:arxiv.org/pdf/1809.10217.pdf
När familjebröllop alla verkar sammanfalla med varandra, fenomenet händer av en anledning. En individ och deras första kusiner tenderar att vara i samma ålder, så deras bröllop sker vanligtvis inom en liknande tidsram. Men bröllop för familjemedlemmar, säg andra och tredje kusiner, tenderar att vara mer spridda. Detta beror på att tiden mellan en generation till nästa varierar, vilket innebär att familjer blir mer spridda från generation till generation.
En ny studie av University of Pennsylvania post-doc Farshid Jafarpour från Institutionen för fysik och astronomi, som arbetar i Andrea Lius laboratorium, avslöjar att variationer i generationstider inte ackumuleras över flera generationer i encelliga organismer, som bakterier. Han föreslår en ny teori, publicerad i Fysiska granskningsbrev , som beskriver hur faktorer som reglerar storleken på enskilda celler påverkar tillväxttakten för en hel befolkning.
Till skillnad från djur och växter, bakterier ökar storleken på sin befolkning genom att växa i storlek och sedan dela sig i hälften för att skapa två nya bakterieceller. Genom att studera bakterier när de delar sig regelbundet, känd som den exponentiella tillväxtfasen, Jafarpour kunde utveckla en modell som matematiskt beskriver denna grundläggande fas av befolkningstillväxt. "Om du vill studera bakterietillväxtens fysik, du vill verkligen ta bort alla andra delar som inte ingår i tillväxtfasen, " han säger.
Jafarpour använde en kombination av matematiska ekvationer, datasimuleringar, och data från biologiska experiment som spårade tillväxten av enskilda bakterieceller. Han blev förvånad över att finna att modellen förutspår att bakterier oscillerar mellan långsammare och snabbare utbrott av tillväxt, i "synkroniserade utbrott av divisioner, "i stället för att befolkningen växer i en konstant takt. Dessa tillväxtoscillationer på befolkningsnivå ger nu en ny, matematiskt sätt för biologer att tänka på och studera befolkningsdynamik.
Tidigare, biologer visste att generationstiden i bakteriepopulationer var direkt relaterad till storleken på enskilda celler. Om en bakterie växer för länge, till exempel, dess dotterceller är större, och de måste dela sig tidigare för att kompensera för storleksskillnaden. Denna process, känd som cellstorleksreglering, avbryter också en del av variationen i generationstiden, vilket håller divisionstiderna synkroniserade med varandra under en mycket längre tid än tidigare förväntat. Det är detta individuella mått på cellstorleksreglering som också verkar orsaka svängningar i tillväxthastigheter som ses i Jafarpours modell.
"Variationen i generationstider har två olika källor:variationen i tillväxt och variationen i division, "Jafarpour förklarar." Det intressanta resultatet är att cellstorleksreglering helt avbryter variationen i division, så det enda som är kvar är variationen i tillväxten av de enskilda cellerna. Och, för det är mindre, svängningarna varar mycket längre än du förväntar dig. "
Denna nya modell kan nu användas av biologer för att få information om variationen i individuella tillväxthastigheter, som är svåra att mäta i laboratoriet men är oerhört viktiga för att studera bakteriell utveckling. Och även om denna modell skulle behöva några ändringar innan den kunde användas för att studera andra arter, Jafarpour tror att att hjälpa biologer att få en bättre förståelse för den fysik som ligger till grund för befolkningstillväxten i bakterier är bara ett av många sätt som fysiken kan stödja det arbete som utförs av biologer.
"Biologin har blivit mer fokuserad på att ta reda på den molekylära grunden för mekanismer sedan 1950 -talet med upptäckten av DNA -strukturen, men nu når vi en nivå där vi måste gå tillbaka och göra fler kvantitativa studier. Fysiker har en lång tradition av att arbeta med verkliga system, veta hur man tillämpar många av de kvantitativa metoderna som utvecklats i matematik och också förstå vilka variabler som är relevanta och vilka variabler inte är, "Säger Jafarpour.