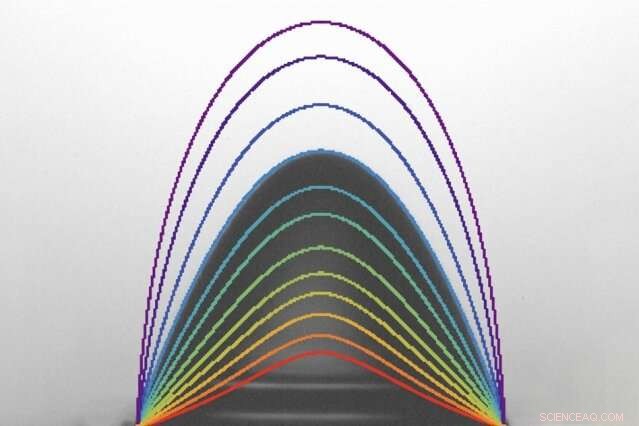
Elektrifierade vattendroppar antar en mängd olika förvrängda former precis innan de spricker, baserat på det elektriska fältets styrka. Profilerna för olika förvrängda droppformer visas, överlagrat på en bild av en viss förvrängd droppe för jämförelse. Upphovsman:Massachusetts Institute of Technology
När en regndroppe faller genom ett åskmoln, den är utsatt för starka elektriska fält som drar och drar i droppen, som en såpbubbla i vinden. Om det elektriska fältet är tillräckligt starkt, det kan göra att droppen spricker isär, skapa böter, elektrifierad dimma.
Forskare började lägga märke till hur droppar beter sig i elektriska fält i början av 1900-talet, mitt i oro över blixtnedslag som skadade nyuppförda kraftledningar. De insåg snart att kraftledningarnas egna elektriska fält fick regndroppar att spränga runt dem, ger en ledande väg för blixten att slå ned. Denna uppenbarelse fick ingenjörer att designa tjockare beläggningar runt kraftledningar för att begränsa blixtnedslag.
I dag, forskare förstår att ju starkare det elektriska fältet är, desto mer sannolikt är det att en droppe inom den spricker. Men, att beräkna den exakta fältstyrkan som kommer att spränga en viss droppe har alltid varit en involverad matematisk uppgift.
Nu, MIT-forskare har funnit att de förhållanden för vilka en droppe spricker i ett elektriskt fält alla kokar ner till en enkel formel, som laget har härlett för första gången.
Med denna enkla nya ekvation, forskarna kan förutsäga den exakta styrkan ett elektriskt fält bör vara för att spränga en droppe eller hålla den stabil. Formeln gäller för tre fall som tidigare analyserats separat:en droppe som klistrats på en yta, glider på en yta, eller fritt svävande i luften.
Deras resultat, publiceras idag i tidskriften Fysiska granskningsbrev , kan hjälpa ingenjörer att justera det elektriska fältet eller storleken på droppar för en rad tillämpningar som är beroende av elektrifierande droppar. Dessa inkluderar teknik för luft- eller vattenrening, rymdframdrivning, och molekylär analys.
"Innan vårt resultat, ingenjörer och forskare var tvungna att utföra beräkningsintensiva simuleringar för att bedöma stabiliteten hos en elektrifierad droppe, " säger huvudförfattaren Justin Beroz, en doktorand vid MIT:s avdelningar för maskinteknik och fysik. "Med vår ekvation, man kan förutsäga detta beteende omedelbart, med en enkel papper-och-penna-beräkning. Detta är till stor praktisk nytta för ingenjörer som arbetar med, eller försöker designa, alla system som involverar vätskor och elektricitet."
Beroz medförfattare är A. John Hart, docent i maskinteknik, och John Bush, professor i matematik.

En vattendroppe, utsatt för ett elektriskt fält med långsamt ökande styrka, spricker plötsligt genom att avge böter, elektrifierad dimma från dess spets. Upphovsman:Massachusetts Institute of Technology
"Något oväntat enkelt"
Droppar tenderar att bilda perfekta små sfärer på grund av ytspänning, den kohesiva kraften som binder vattenmolekyler vid en droppes yta och drar molekylerna inåt. Droppen kan förvrängas från sin sfäriska form i närvaro av andra krafter, såsom kraften från ett elektriskt fält. Medan ytspänningen verkar för att hålla ihop en droppe, det elektriska fältet fungerar som en motkraft, drar utåt på droppen när laddning bygger på dess yta.
"Vid något tillfälle, om det elektriska fältet är tillräckligt starkt, droppen kan inte hitta en form som balanserar den elektriska kraften, och vid den tidpunkten, den blir instabil och spricker, Beroz förklarar.
Han och hans team var intresserade av ögonblicket precis innan de brast, när droppen har förvrängts till sin kritiskt stabila form. Teamet startade ett experiment där de långsamt fördelade vattendroppar på en metallplatta som elektrifierades för att producera ett elektriskt fält, och använde en höghastighetskamera för att registrera de förvrängda formerna för varje droppe.
"Experimentet är riktigt tråkigt till en början - du ser droppen sakta ändra form, och så plötsligt spricker det bara, " säger Beroz.
Efter att ha experimenterat på droppar av olika storlekar och under olika elektriska fältstyrkor, Beroz isolerade videoramen precis innan varje droppe brast, skisserade sedan dess kritiskt stabila form och beräknade flera parametrar som droppens volym, höjd, och radie. Han plottade data från varje droppe och fann, till hans förvåning, att de alla föll längs en omisskännligt rak linje.
"Från en teoretisk synvinkel, det var ett oväntat enkelt resultat med tanke på problemets matematiska komplexitet, " säger Beroz. "Det antydde att det kan finnas en förbisedd, ändå enkelt, sätt att beräkna bristningskriteriet för dropparna."
Volym över höjd
Fysiker har länge känt till att en vätskedroppe i ett elektriskt fält kan representeras av en uppsättning kopplade olinjära differentialekvationer. Dessa ekvationer, dock, är otroligt svåra att lösa. För att hitta en lösning måste man bestämma konfigurationen av det elektriska fältet, formen på droppen, och trycket inuti droppen, samtidigt.
"Detta är vanligtvis fallet inom fysiken:det är lätt att skriva ner de styrande ekvationerna men väldigt svårt att faktiskt lösa dem, " säger Beroz. "Men för dropparna, det visar sig att om du väljer en speciell kombination av fysiska parametrar för att definiera problemet från början, en lösning kan härledas på några rader. Annat, det är omöjligt."
Fysiker som försökte lösa dessa ekvationer tidigare gjorde det genom att räkna in, bland andra parametrar, en droppes höjd – ett enkelt och naturligt val för att karakterisera en droppes form. Men Beroz gjorde ett annat val, omforma ekvationerna i termer av en droppes volym snarare än dess höjd. Detta var nyckelinsikten för att omformulera problemet till en lättlöslig formel.
"Under de senaste 100 åren, konventionen var att välja höjd, " säger Beroz. "Men när en droppe deformeras, dess höjd ändras, och därför är problemets matematiska komplexitet inneboende i höjden. Å andra sidan, en droppes volym förblir fixerad oavsett hur den deformeras i det elektriska fältet."
Genom att formulera ekvationerna med bara parametrar som är "fasta" i samma mening som en droppes volym, "det komplicerade, olösliga delar av ekvationen tar bort, lämnar en enkel ekvation som matchar experimentresultaten, " säger Beroz.
Specifikt, den nya formeln som teamet tog fram relaterar fem parametrar:en droppes ytspänning, radie, volym, elektrisk fältstyrka, och den elektriska permittiviteten hos luften som omger droppen. Om du kopplar in någon av fyra av dessa parametrar i formeln beräknas den femte.
Beroz säger att ingenjörer kan använda formeln för att utveckla tekniker som elektrosprayning, vilket involverar sprängning av en droppe som hålls vid öppningen av ett elektrifierat munstycke för att producera en fin spray. Elektrosprutning används vanligtvis för att aerosolisera biomolekyler från en lösning, så att de kan passera genom en spektrometer för detaljerad analys. Tekniken används också för att producera dragkraft och driva satelliter i rymden.
"Om du designar ett system som involverar vätskor och elektricitet, det är väldigt praktiskt att ha en sådan här ekvation, som du kan använda varje dag, " säger Beroz.
Den här historien återpubliceras med tillstånd av MIT News (web.mit.edu/newsoffice/), en populär webbplats som täcker nyheter om MIT-forskning, innovation och undervisning.