Topologiska tillstånd av materia är materiefaser som går utöver Landau symmetribrytande teori, som kännetecknas av topologiska invarianter och topologiska kanttillstånd. Fysikern David J. Thouless, i samarbete med F. Duncan, M. Haldane och J. Michael Kosterlitz, avslöjade dessa unika materiella tillstånd, fick Nobelpriset i fysik 2016.

Sedan deras upptäckt, topologiska tillstånd av materia har blivit i fokus för ett växande antal studier. Forskare från olika områden söker nu aktivt efter dessa stater, som att observera dem kan både bredda vår nuvarande förståelse för ovanliga materiella tillstånd och underlätta förverkligandet av topologisk kvantberäkning.

I en nyligen genomförd studie ett team av forskare vid Tsinghua University, Shanxi University och South China Normal University kunde observera topologiska magnonisolatortillstånd i en supraledande krets. Deras papper, publicerad i Fysiska granskningsbrev , är den första som visar hur en qubit -kedja flexibelt kan ställas in i topologiskt triviala eller icke -triviala magnonisolatortillstånd.

"Begreppet topologiska tillstånd kommer ursprungligen från elektroniska system i solid state, "Feng Mei, en av forskarna som genomförde studien, berättade för Phys.org. "Det har nu utökats till olika artificiella bosoniska system, inklusive ultrakylda atomer fångade i optiska gitter, konstgjorda fotoniska och fononiska gitter. "

Under de senaste åren, forskare har gjort betydande framsteg när det gäller att uppnå skalbar kvantberäkning med hjälp av supraledande kretsar. Till exempel, IBM och Google påstod båda att ha framgångsrikt konstruerat qubit -galler med 50 och 72 qubits, respektive. Inspirerad av dessa fynd, Mei och hans kollegor började undra om de kunde inse ett topologiskt tillstånd i en qubit -kedja, uppnå ett "topologiskt skydd" för qubiterna.

"I vårt arbete, för första gången, vi visar att supraledande qubit -kedjor kan stödja topologiska magnonisolatortillstånd och ha topologiskt skydd, "Mei sa." Vårt arbete visar att superledande kvantdatorplattform också kan användas för att förverkliga topologiska tillstånd av materia. Dessutom, det öppnar möjligheter för att implementera topologiskt skyddad kvantinformationsbehandling. "

I fysik av kondenserad materia, magnoner är kollektiva excitationer av elektronernas spinnkedja i ett kristallgitter. En topologisk magnonisolator, å andra sidan, är ett nytt topologiskt tillstånd associerat med magnoner, som kännetecknas av den topologiska invarianten.

Systemet som undersöks av Mei och hans kollegor har ett topologiskt lindningsnummer associerat med endimensionella system. Med andra ord, när dess topologiska lindningsnummer är något annat än noll, systemet är i sina topologiska isolatortillstånd.

"Enligt korrespondens i stor utsträckning, det topologiska lindningsnumret utan noll garanterar förekomsten av topologiska kanttillstånd, "Luyan Sun, en annan forskare som är involverad i studien, berättade för Phys.org. "Således, topologiskt lindningsnummer och topologiskt kanttillstånd är de två kännetecknande kännetecknen för topologiska isolatorer. Dock, de har inte observerats samtidigt i några topologiska system tidigare. "

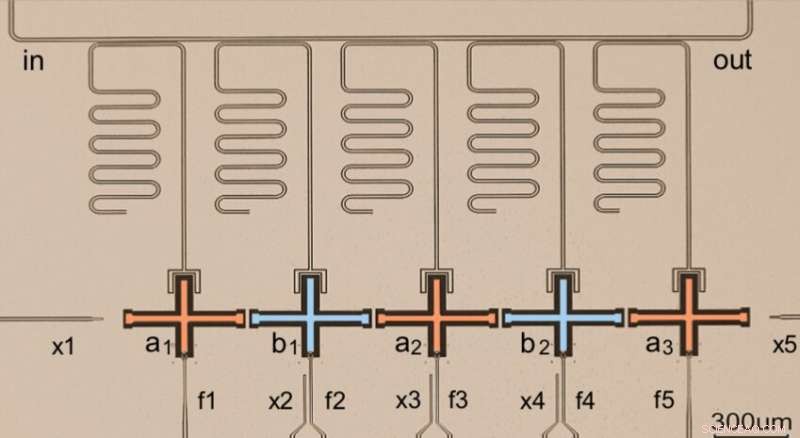
I deras studie, Mei och Sun använde en kedja av qubits, var och en av dessa qubits är en supraledande krets. Som de visade i en tidigare studie, den effektiva kopplingen mellan angränsande qubits kan ställas in genom parametrisk modulering av qubits frekvenser.

"Den effektiva kopplingsstyrkan kännetecknar energiutbyteshastigheten mellan angränsande qubits, "Sun sa." Den kan ställas in för att vara godtyckligt mindre än den statiska kopplingsstyrkan som bestäms av enhetens geometri. I vår enhet, alla qubits är frekvensinställbara och kan styras av individuella externa fluxförspänningslinjer. "

Deras inställning och procedur gjorde det möjligt för forskarna att helt enkelt ställa in qubit-kedjan i topologiska och icke-topologiska tillstånd (dvs att slå på eller stänga av dessa tillstånd) genom att ändra qubit-kopplingskonfigurationerna. I deras experiment, de upphetsade helt enkelt en av qubiterna (dvs en magnon) och övervakade sedan dess dynamik inom qubit -kedjan. Observationerna de samlade tillät dem att undersöka både systemets topologiska lindningsnummer och dess topologiska kanttillstånd.

"Vi överväger bara en-qubit excitation och inser de icke-interagerande topologiska tillstånden, "Sade Mei." Om vi ​​överväger att lägga flera qubit -excitationer i qubit -kedjan, interagerande symmetri-skyddade topologiska tillstånd kan också realiseras och utforskas i detta system. Våra fynd innebär att en supraledande qubit-kedja kan användas som en mångsidig plattform för att utforska olika icke-interagerande och interagerande symmetri-skyddade topologiska tillstånd av materia. "

Den senaste studien utförd av Mei, Sun och deras kollegor visar att topologiska tillstånd av materia också kan uppstå i en supraledande qubit -kedja. Dessutom, det ger värdefull insikt om förverkligandet av topologiskt skydd för qubits i en kedja. Detta kan främja utvecklingen av topologiskt skyddade tekniker för kvantinformationsbehandling.

I deras framtida arbete, forskarna planerar att inse symmetri-skyddade interagerande topologiska tillstånd av materia. Dessutom, de hoppas kunna avslöja sätt att implementera topologiskt skyddade kvantinformationsbehandlingsuppgifter med hjälp av supraledande qubit -kedjor.

"Symmetri-skyddade interagerande topologiska tillstånd är viktiga interagerande topologiska tillstånd av materia och deras förverkligande är för närvarande fortfarande en stor utmaning, "Mei sa." Superledande qubit -kedjor med flera qubit -excitationer ger en naturlig plattform för att förverkliga sådana tillstånd. Med det topologiska skyddet som de topologiska tillstånden ger, vi kommer att fortsätta att studera hur man förverkligar topologiskt skyddade kvantinformationsbehandlingsuppgifter, såsom topologiskt skyddad kvanttillståndsöverföring. "

© 2019 Science X Network