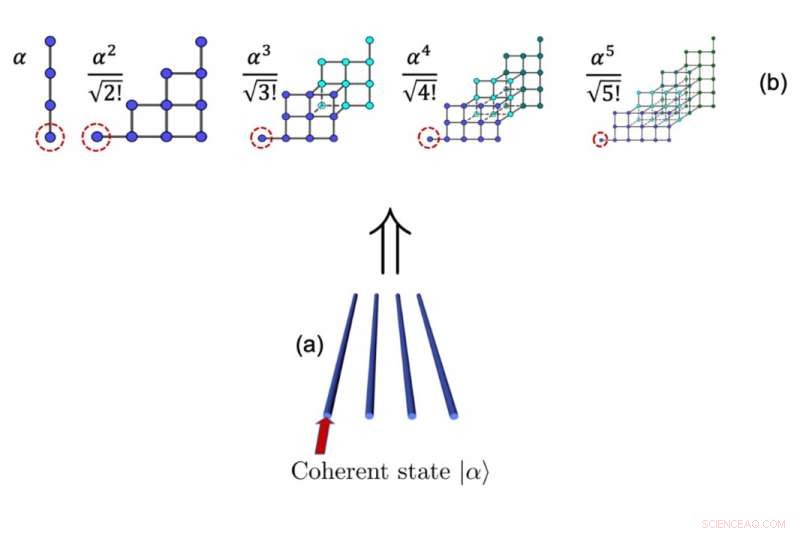
(a) Schema för en fyra-vågledaruppsättning exciterad av ett koherent tillstånd \α〉 (röd pil indikerar den exciterade vågledaren). (b) Syntetiska grafer som kommer fram från det koherenta tillståndsexciteringen av systemet i (a). Eftersom vi är spännande med ett sammanhängande tillstånd, sannolikhetsamplituderna för varje händelse ges av αn/ √n! Kredit:MBI
I fysik, ett mycket intuitivt sätt att beskriva utvecklingen av ett system sker via specifikation av funktioner för de spatiotemporala koordinaterna. Än, det finns ofta andra frihetsgrader i termer av vilka de fysiska enheterna som hör till en mängd olika strukturer kan ses utvecklas och som inte är mottagliga för en beskrivning via rumsliga koordinater.
Detta är just idén med syntetiska dimensioner:samexisterande ramverk där en vågfunktion, definieras i specifika frihetsgrader, tar en annan form som 'bor' i en domän med mycket högre dimensioner än vad strukturernas (skenbara) geometri skulle antyda. Detta tillvägagångssätt är ganska tilltalande eftersom det kan användas för att komma åt och undersöka dimensioner bortom vår 3-dimensionella värld, t.ex. 5-dimensionell eller 8-dimensionell, etc.
I vårt senaste arbete har vi visat att en mängd högdimensionella syntetiska gitter naturligt dyker upp i (abstrakt) fotonnummerrymd när ett fotoniskt gitter med flera portar exciteras av N oskiljbara fotoner. Mer exakt, Fock-representationen av N-fotontillstånd i system som består av M evanescent kopplade enkelmodsvågledare ger ett nytt abstraktionslager, där de associerade tillstånden kan visualiseras som energinivåerna för en syntetisk atom. I full analogi med vanliga atomer, sådana syntetiska atomer har tillåtna och otillåtna övergångar mellan dess energinivåer.
Dessa koncept har långtgående implikationer eftersom de öppnar en väg till det samtidiga förverkligandet av, i princip, ett oändligt antal gitter och grafer med olika antal noder och många dimensioner. Denna möjlighet är ganska tilltalande för att realisera parallella kvantslumpmässiga vandringar där motsvarande vandrare kan utföra olika antal steg på olika, plana och icke-plana, flerdimensionella grafer som beror på antalet fotoner som är involverade i varje process. Dessa kvantvandringar kan implementeras, till exempel, genom att excitera ett enkelt fyrvågsledarsystem med en standard kvantljuskälla som omfattar oändliga koherenta överlagringar av tillstånd, t.ex. ett koherent tillstånd |α> . Liknande, den symmetriska exciteringen av ett tvåvågsledarsystem med identiska fotoner, när man ser den på rätt sätt i abstrakt utrymme, presenterar fenomenen diskret diffraktion och Bloch-svängningar.
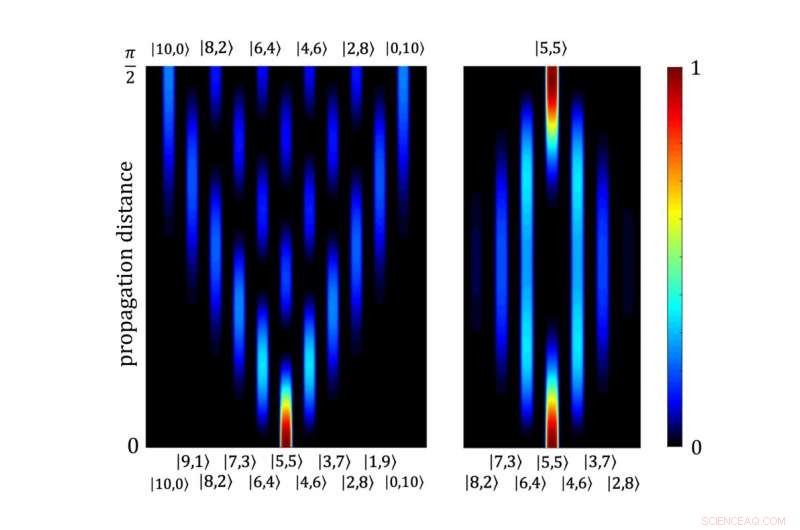
Diskret diffraktion och Bloch-oscillationer i abstrakt Fock-rymd som framträder från ett enkelt tvåvågledarsystem för stråldelare exciterat av tiofotontillståndet l5, 5. Kredit:MBI