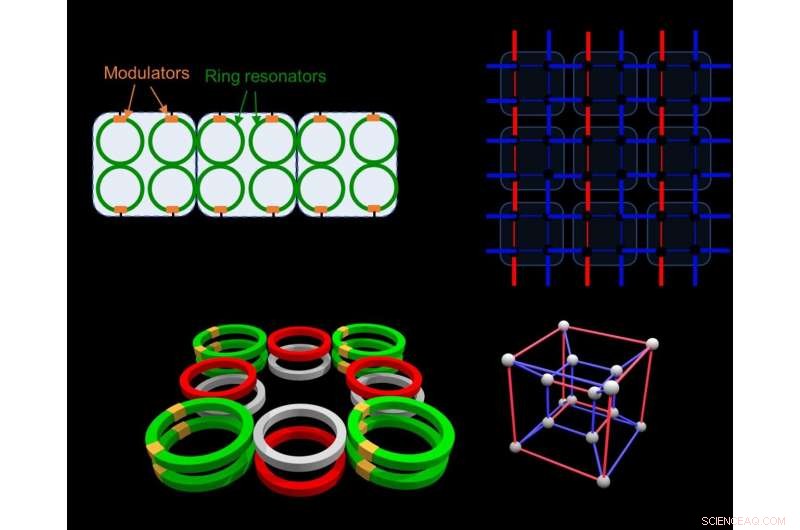
a, En uppsättning kopplade ringresonatorer (grön), var och en med en inbäddad elektrooptisk modulator (orange). b, Motsvarande galler i verkliga och syntetiska dimensioner, x och frekvens, respektive. Gallret visar topologiskt beteende av högre ordning, såsom förekomsten av hörnlägen. (c), Real-space struktur för att realisera en fjärde ordningens topologisk isolator. (d), Motsvarande gitter i verkligt och syntetiskt utrymme är en hyperkub (en fyrdimensionell kub), där den inre 3D-kuben motsvarar botten av ringar i (c), och den yttre kuben motsvarar den översta raden av ringar i (c). Kredit:av Avik Dutt, Momchil Minkov, Ian A.D. Williamson, och Shanhui Fan
Topologiska isolatorer har varit ett spännande forskningsfält med grundläggande intresse såväl som praktiska tillämpningar som robust transport av elektroner och ljus, och topologisk kvantberäkning. Kännetecknet för sådana konventionella topologiska isolatorer är närvaron av ledande gränslägen som har en dimension lägre än det isolerande bulksystemet som är värd för dem - till exempel ett endimensionellt kantläge vid gränsen av ett tvådimensionellt system, eller ett tvådimensionellt yttillstånd vid gränsen för ett tredimensionellt system. År 2017, forskare generaliserade detta koncept för att förutsäga en ny fas av materia som kallas högre ordningens topologiska isolatorer (HOTIs), som stöder 'hörnlägen' — t.ex. ett nolldimensionellt läge i ett tvådimensionellt system. Sedan dess, det har varit flera experimentella demonstrationer av denna nya HOTI-fas, de flesta involverar komplicerade geometrier. Dessutom, dessa tidigare system är fasta — d.v.s. man kan inte dynamiskt byta eller ställa in deras topologiska beteende av högre ordning när de väl är tillverkade.
I en ny artikel publicerad i Ljusvetenskap och tillämpningar , ett team av forskare, ledd av professor Shanhui Fan från Stanford University, USA, och medarbetare har föreslagit ett sätt att realisera sådan högre ordnings topologi och hörntillstånd med hjälp av ett framväxande koncept som kallas "syntetiska dimensioner, ' i enklare strukturer och på ett dynamiskt inställbart sätt. Vanligtvis, partiklar som fotoner och elektroner antas röra sig längs de tre riktningarna - x, y och z, eller längd, bredd och djup. Tänk om man kunde föreställa sig fotonernas rörelse bortom dessa tre "riktiga" riktningar? Teamet kallar dessa extra rörelseriktningar "syntetiska dimensioner."
För att göra detta konceptuella språng från de tre verkliga dimensionerna till syntetiska dimensioner, de utnyttjade inre egenskaper som är inneboende för alla fotoner – ljusets frekvens eller färg, som avgör hur mycket energi en foton bär. Tidigare arbete från Stanford-teamet och andra grupper har visat konventionella (första ordningens) topologiska faser med hjälp av detta koncept med syntetiska dimensioner, inklusive spännande fysiska fenomen som quantum Hall-effekten. Dock, topologi av högre ordning hade varit utom räckhåll för syntetiska dimensioner tills nu, även om HOTIs högdimensionella karaktär är mycket väl lämpad för idén om syntetiska dimensioner.
För att konstruera den högre ordningens topologiska isolatorn, forskarna föreslår att man använder en uppsättning ringresonatorer som är kopplade till varandra i ett specifikt arrangemang. Varje ringresonator är i huvudsak en tunn tråd av ett genomskinligt material som är öglad på sig själv, så att en foton kan gå runt slingan många gånger. Ett par av två identiska ringresonatorer bildar tillsammans en 'fotonisk molekyl, ' precis som två väteatomer bildar en diatomisk molekyl. Genom att arrangera flera sådana fotoniska molekyler längs en linje, en andra ordningens topologisk isolator för fotoner kan bildas. Precis som i verkliga dimensioner kan man styra om en foton rör sig till höger eller vänster (säg i x-riktningen), ringresonatorn kan i syntetiska dimensioner styra om en foton rör sig uppåt eller nedåt i frekvens. Sådan rörelse i frekvens uppnås med en annan fotonisk komponent som kallas en modulator - en enhet som kan ändra materialets brytningsindex vid höga hastigheter, vilket gör dem väsentliga för dagens optiska telekommunikationsnät.
Nästa, teamet förutsäger hur kännetecknet för topologi av högre ordning – hörnlägena – kan ses i detta system genom att sända specifika frekvenser av laserljus in i uppsättningen fotoniska molekyler. För dessa hörnlägen, ljus är begränsat till hörnet av den tvådimensionella strukturen som består av en reell dimension och en syntetisk frekvensdimension, och det finns nästan inget ljus i resten av strukturen.
"En stor fördel med syntetiska dimensioner är flexibiliteten med vilken olika rattar kan styras för att justera systemparametrar. Genom att styra styrkan och timingen av den elektroniska signalen som appliceras på modulatorerna i fotonmolekylerna, vi visade hur dessa hörnlägen kunde slås på och av. Med andra ord, du kan byta systemet från att ha högre ordning topologi till att ha ingen topologi, dynamiskt. Denna förmåga är oöverträffad i typiska elektroniska eller fotoniska system, " säger författarna.
Med syntetiska dimensioner, man kan tänka sig att bygga mycket högdimensionella topologiska isolatorer, som är svåra att bygga eller ens föreställa sig i det verkliga rummet eftersom vi lever i en tredimensionell värld. Som ett exempel, teamet konstruerar en fjärde ordningens topologisk isolator i ett fyrdimensionellt system, vilket inte har förutspåtts tidigare eftersom det ligger utanför det tredimensionella verkliga rummets räckvidd.
"Våra recept beskriver hur man använder syntetiska dimensioner för att implementera mycket komplicerade högdimensionella fenomen, inklusive extremt högklassiga topologiska isolatorer och andra exotiska faser av ljus och materia, i mycket enklare system, och dynamiskt kontrollera deras egenskaper nästan efter behag. Experimentella förverkliganden av detta koncept ligger väl inom räckhåll för dagens toppmoderna fotoniska teknik, ", tillägger forskarna.