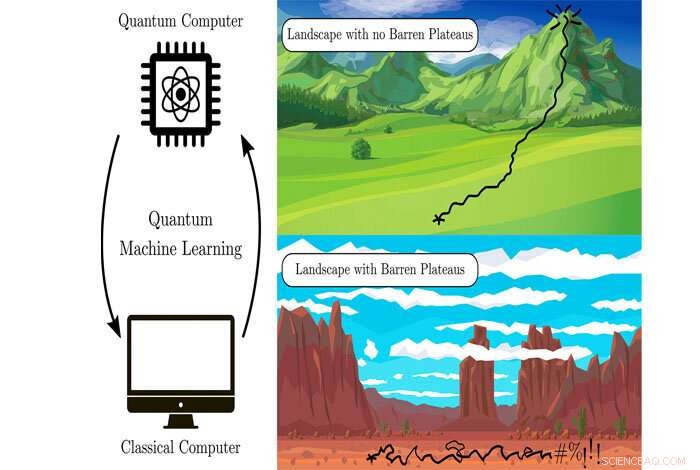
En karg platå är ett träningsproblem som uppstår i optimeringsalgoritmer för maskininlärning när problemlösningsutrymmet blir platt när algoritmen körs. Forskare vid Los Alamos National Laboratory har utvecklat teorem för att bevisa att varje given algoritm kommer att undvika en karg platå när den skalas upp för att köras på en kvantdator. Kredit:Los Alamos National Laboratory 19 mars, 2021
Många maskininlärningsalgoritmer på kvantdatorer lider av den fruktade "karga platån" av olöslighet, där de hamnar i återvändsgränder i optimeringsproblem. Denna utmaning hade varit relativt outstuderad – fram till nu. Rigoröst teoretiskt arbete har etablerat teorem som garanterar om en given maskininlärningsalgoritm kommer att fungera när den skalas upp på större datorer.
"Arbetet löser ett nyckelproblem med användbarhet för kvantmaskininlärning. Vi har noggrant bevisat villkoren under vilka vissa arkitekturer av variationsmässiga kvantalgoritmer kommer eller inte kommer att ha karga platåer när de skalas upp, sa Marco Cerezo, huvudförfattare på tidningen publicerad i Naturkommunikation idag av ett team från Los Alamos National Laboratory. Cerezo är en post doc som forskar om kvantinformationsteori vid Los Alamos. "Med våra teorem, du kan garantera att arkitekturen kommer att vara skalbar till kvantdatorer med ett stort antal qubits."
"Vanligtvis har tillvägagångssättet varit att köra en optimering och se om det fungerar, och det ledde till trötthet bland forskare på området, sa Patrick Coles, en medförfattare till studien. Att upprätta matematiska teorem och härleda första principer tar bort gissningsarbetet med att utveckla algoritmer.
Los Alamos-teamet använde den vanliga hybridmetoden för variationsmässiga kvantalgoritmer, träning och optimering av parametrarna på en klassisk dator och utvärdering av algoritmens kostnadsfunktion, eller måttet på algoritmens framgång, på en kvantdator.
Maskininlärningsalgoritmer översätter en optimeringsuppgift – säg, hitta den kortaste vägen för en resande säljare genom flera städer – till en kostnadsfunktion, sa medförfattaren Lukasz Cincio. Det är en matematisk beskrivning av en funktion som kommer att minimeras. Funktionen når sitt lägsta värde endast om du löser problemet.
De flesta kvantvariationsalgoritmer initierar sin sökning slumpmässigt och utvärderar kostnadsfunktionen globalt över varje qubit, vilket ofta leder till en karg platå.
"Vi kunde bevisa att om du väljer en kostnadsfunktion som tittar lokalt på varje enskild qubit, då garanterar vi att skalningen inte kommer att resultera i en omöjligt brant kurva av tid kontra systemstorlek, och kan därför tränas, " sa Coles.
En kvantvariationsalgoritm sätter upp ett problemlösningslandskap där topparna representerar systemets höga energipunkter, eller problem, och dalarna är de låga energivärdena. Svaret ligger i den djupaste dalen. Det är grundtillståndet, representeras av funktionen minimerade kostnad. För att hitta lösningen, Algoritmen tränar sig själv om landskapet, och därigenom navigera till den låga platsen.
"Människor har föreslagit kvantneurala nätverk och benchmarkat dem genom att göra småskaliga simuleringar av 10s (eller färre) få qubits, " sa Cerezo. "Problemet är att du kommer inte att se den karga platån med ett litet antal qubits, men när du försöker skala upp till fler qubits, det verkar som. Sedan måste algoritmen omarbetas för en större kvantdator."
En karg platå är ett träningsproblem som uppstår i optimeringsalgoritmer för maskininlärning när problemlösningsutrymmet blir platt när algoritmen körs. I det läget, Algoritmen kan inte hitta den nedåtgående lutningen i vad som verkar vara ett särdragslöst landskap och det finns ingen tydlig väg till energiminimum. Saknar landskapsdrag, maskininlärningen kan inte träna sig själv för att hitta lösningen.
"Om du har en karg platå, allt hopp om kvanthastighet eller kvantfördel är förlorat, " sa Cerezo.
Los Alamos-lagets genombrott tar ett viktigt steg mot kvantfördelar, när en kvantdator utför en uppgift som skulle ta oändligt lång tid på en klassisk dator. Att uppnå kvantfördelar beror på kort sikt på att skala upp variationsmässiga kvantalgoritmer. Dessa algoritmer har potentialen så löser praktiska problem när kvantdatorer på 100 qubits eller mer blir tillgängliga – förhoppningsvis snart. Kvantdatorer maxar för närvarande på 65 qubits. En qubit är den grundläggande informationsenheten i en kvantdator, som bitar finns i en klassisk digital dator.
"Det hetaste ämnet i bullriga kvantdatorer i mellanskalig skala är variationsmässiga kvantalgoritmer, eller kvantmaskininlärning och kvantneurala nätverk, "Sade Coles. "De har föreslagits för tillämpningar från att lösa strukturen hos en molekyl i kemi till att simulera dynamiken hos atomer och molekyler och factoringtal."