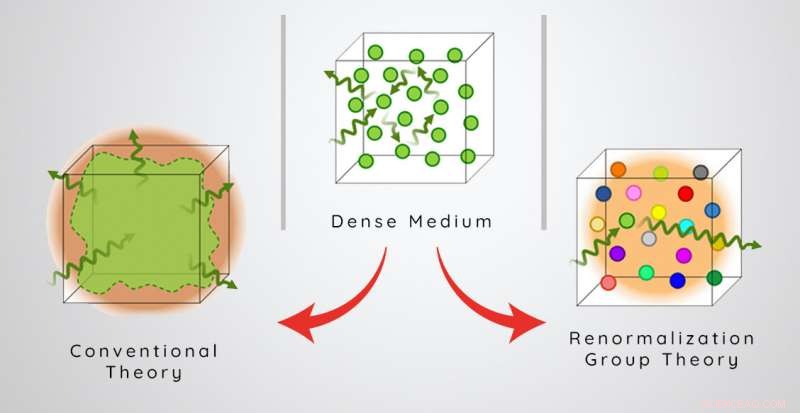
Schematisk illustration av den optiska responsen hos ett tätt atomärt medium sett av traditionella teorier kontra RG-teorin. Kredit:ICFO
Pink Floyds Dark Side of the Moon-omslag, röstade fram det största klassiska rockalbumet genom tiderna, tänkt att skildra ljusets prisma och spridning i en regnbåge som en viss metaforisk symbolik och en ljusshow som aldrig firades. Dock, de var verkligen inte medvetna om att denna bild skulle användas av många för att illustrera begreppet brytningsindex och hur ljus ändrar hastighet och riktning när det möter ett annat medium.
Trots att konceptet inte var korrekt, den förmedlade budskapet att ljus ändrar sin hastighet när det flyttar in i ett annat medium, och att de olika hastigheterna i olika färger gör att vitt ljus sprids i dess olika komponenter. Denna förändring i hastighet är relaterad till brytningsindex, ett enhetslöst tal som representerar förhållandet mellan ljusets hastighet i vakuum och ljusets hastighet i ett medium.
I allmänhet, alla material med positivt brytningsindex har värden nära 1 för synligt ljus. Huruvida detta bara är en slump eller återspeglar någon djupare fysik har aldrig förklarats.
Nu, i en nyligen publicerad studie Fysisk granskning X och framhävd av redaktionen, ICFO-forskarna Francesco Andreoli och ICREA Prof. vid ICFO Darrick Chang, i samarbete med forskare från Princeton University, University of Chicago och Institut d'Optique, har undersökt och förklarat varför brytningsindexet för en utspädd atomgas endast kan nå ett maximalt värde på 1,7, oavsett hur hög tätheten av atomer blir.
Detta resultat står i kontrast till konventionella läroboksteorier, som förutspår att ju mer material det finns, desto större kan den optiska responsen och brytningsindex vara. Utmaningen i att förstå problemet korrekt måste hantera multipel spridning av ljus - alla de komplexa vägar som ljuset kan passera inuti ett medium - och den resulterande störningen. Detta kan få varje enskild atom att se en lokal ljusintensitet som är mycket annorlunda än intensiteten som skickas in, och som varierar beroende på geometrin hos atomerna som omger den. Istället för att ta itu med de komplexa mikroskopiska detaljerna i denna granularitet, läroböcker antar ofta på något sätt att denna granularitet och dess effekter på ljus kan jämnas ut.
I kontrast, lagen använder sig av en teori, kallad renormaliseringsgrupp med stark störning (RG), vilket gör det möjligt för dem att fånga granularitet och multipla spridningseffekter på ett enkelt sätt. Denna teori visar att det optiska svaret hos en given atom påverkas oproportionerligt mycket av sin enstaka närmaste granne på grund av närfältsinteraktioner, vilket är anledningen till att typiska utjämningsteorier misslyckas. Den fysiska effekten av närfältets interaktioner är att producera en inhomogen utvidgning av atomresonansfrekvenser, där mängden breddning växer med densitet. Således, oavsett hur hög den fysiska tätheten av atomer är, inkommande ljus av vilken frekvens som helst kommer bara att se ungefär 1 nästan resonant atom per kubikvåglängd för att effektivt spridas, vilket begränsar brytningsindexet till dess maximala värde på 1,7.
Mer allmänt, denna studie tyder på att RG-teorin skulle kunna utgöra ett nytt mångsidigt verktyg för att förstå det utmanande problemet med multipel spridning av ljus i nästan resonanta störda medier, inklusive i de olinjära och kvantregimerna. Det visar också löftet om att försöka förstå gränserna för brytningsindex för verkliga material, börjar nerifrån och upp från de individuella atomerna som de består av.