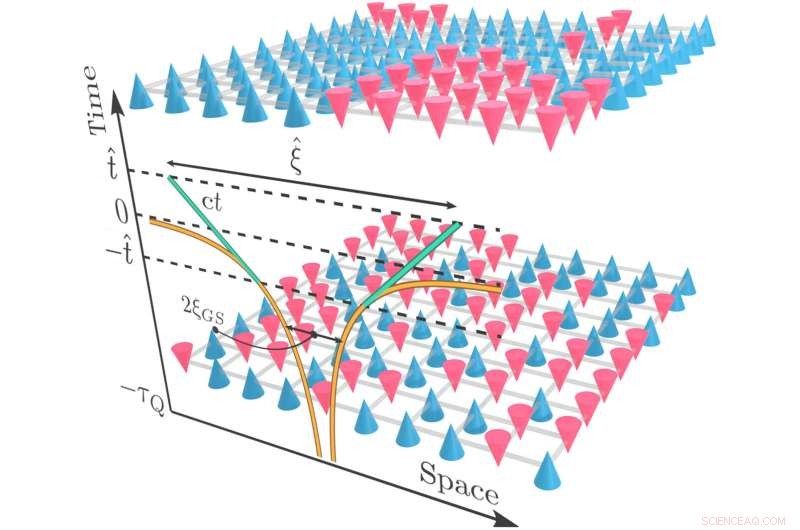
Schematisk skildring av dynamiken över en fasövergång i en tvådimensionell spin-1/2-modell. I det initiala paramagnetiska tillståndet (nederst) är spinn i linje med riktningen för det tvärgående magnetfältet. En mätning av snurrkonfigurationen i det tillståndet längs ordningsriktningen skulle då typiskt ge ett slumpmässigt mönster av snurr som pekar uppåt (blå koner) eller nedåt (röda koner). Efter en långsam ramp över en kvantkritisk punkt, utvecklar systemet en kvantöverlagring av ferromagnetiska domäner, som, vid mätning av spinnkonfigurationer längs ordningsriktningen, vanligtvis kommer att ge en kollaps på en mosaik av sådana domäner (överst). På framsidan inkluderar vi tillväxten av det ferromagnetiska korrelationsområdet som en funktion av tiden t från t =−τQ när rampen fortskrider över den kritiska regimen med den kritiska punkten belägen vid t =0. Läkningslängden ξˆ som bestämmer storleken på domäner i Kibble-Zurek (KZ) mekanismen ställs in på den karakteristiska tiden ∣∣t∣
Ett internationellt team av fysiker, med deltagande av universitetet i Augsburg, har för första gången bekräftat en viktig teoretisk förutsägelse inom kvantfysik. Beräkningarna för detta är så komplexa att de hittills visat sig vara alltför krävande även för superdatorer. Forskarna lyckades dock förenkla dem avsevärt med metoder från maskininlärning. Studien förbättrar förståelsen av grundläggande principer för kvantvärlden. Den har publicerats i tidskriften Science Advances .
Beräkningen av rörelsen för en enda biljardboll är relativt enkel. Det är dock mycket svårare att förutsäga banorna för en mängd gaspartiklar i ett kärl som ständigt kolliderar, saktas ner och avleds. Men tänk om det inte ens alls är klart exakt hur snabbt varje partikel rör sig, så att de skulle ha otaliga möjliga hastigheter vid varje given tidpunkt, bara olika i deras sannolikhet?
Situationen är liknande i kvantvärlden:Kvantmekaniska partiklar kan till och med ha alla potentiellt möjliga egenskaper samtidigt. Detta gör tillståndsutrymmet för kvantmekaniska system extremt stort. Om du siktar på att simulera hur kvantpartiklar interagerar med varandra, måste du överväga deras fullständiga tillståndsrum.
"Och det är extremt komplext", säger prof. Dr. Markus Heyl från Institutet för fysik vid universitetet i Augsburg. "Beräkningsansträngningen ökar exponentiellt med antalet partiklar. Med mer än 40 partiklar är den redan så stor att inte ens de snabbaste superdatorerna klarar av det. Detta är en av kvantfysikens stora utmaningar."
Neurala nätverk gör problemet hanterbart
För att förenkla detta problem använde Heyls grupp metoder från området maskininlärning - artificiella neurala nätverk. Med dessa kan det kvantmekaniska tillståndet omformuleras. "Detta gör det hanterbart för datorer", förklarar Heyl.
Med den här metoden har forskarna undersökt en viktig teoretisk förutsägelse som hittills har förblivit en enastående utmaning - kvantmekanismen Kibble-Zurek. Den beskriver det dynamiska beteendet hos fysiska system vid vad som kallas en kvantfasövergång. Ett exempel på en fasövergång från den makroskopiska och mer intuitiva världen är övergången från vatten till is. Ett annat exempel är avmagnetiseringen av en magnet vid höga temperaturer.
Om du går tvärtom och kyler materialet börjar magneten bildas igen under en viss kritisk temperatur. Detta sker dock inte jämnt över hela materialet. Istället skapas många små magneter med olika riktade nord- och sydpoler samtidigt. Således är den resulterande magneten faktiskt en mosaik av många olika, mindre magneter. Fysiker säger också att det innehåller defekter.
Kibble-Zurek-mekanismen förutsäger hur många av dessa defekter som kan förväntas (med andra ord, hur många minimagneter som materialet så småningom kommer att bestå av). Det som är särskilt intressant är att antalet dessa defekter är universella och därmed oberoende av mikroskopiska detaljer. Följaktligen beter sig många olika material exakt identiskt, även om deras mikroskopiska sammansättning är helt annorlunda.
Kibble-Zurek-mekanismen och bildandet av galaxer efter Big Bang
Kibble-Zurek-mekanismen introducerades ursprungligen för att förklara bildandet av struktur i universum. Efter Big Bang var universum till en början helt homogent, vilket innebär att den värdmateria fördelades perfekt jämnt. Under lång tid har det varit oklart hur galaxer, solar eller planeter kunde ha bildats ur ett så homogent tillstånd.
I detta sammanhang ger Kibble-Zurek-mekanismen en förklaring. När universum kyldes ner utvecklades defekter på liknande sätt som magneter. Under tiden är dessa processer i den makroskopiska världen väl förstådda. Men det finns en typ av fasövergång för vilken det ännu inte har varit möjligt att verifiera mekanismens giltighet - nämligen de kvantfasövergångar som redan nämnts tidigare. "De finns bara vid den absoluta nolltemperaturen på -273 grader Celsius", förklarar Heyl. "Så fasövergången sker inte under kylning, utan genom förändringar i interaktionsenergin - man skulle kanske kunna tänka sig att variera trycket."
Forskarna har nu simulerat en sådan kvantfasövergång på en superdator. De kunde därmed för första gången visa att Kibble-Zurek-mekanismen även gäller i kvantvärlden. "Det var inte på något sätt en självklar slutsats", säger Augsburg-fysikern. "Vår studie gör det möjligt för oss att bättre beskriva dynamiken i kvantmekaniska system för många partiklar och därmed förstå mer exakt reglerna som styr denna exotiska värld." + Utforska vidare