Periodiska kedjeliknande nanostrukturer används i stor utsträckning inom nanoelektronik. Vanligtvis, kedjeelement inkluderar kvantringar, kvantprickar, eller kvantgrafer. En sådan struktur gör det möjligt för elektroner att röra sig längs kedjan, i teorin, obegränsat. Problemet är att vissa applikationer kräver lokaliserade elektroner - dessa är inte längre i ett kontinuerligt energispektrum utan i ett diskret energispektrum, istället.

Nu, en ny studie av ryska forskare identifierar sätt att störa periodiciteten hos en modell nanostruktur för att erhålla det önskade diskreta spektrumet med lokaliserade elektroner. Dessa fynd av Dr Dmitry A. Eremin från Mordovian State University i Saransk, Ryssland, och kollegor har publicerats i European Physical Journal B .

Teoretiska beräkningar på nanosystem spelar en viktig roll i förutsägelsen av elektriska transportegenskaper. Författarna skapade teoretiska modeller av enheter i nanometrisk skala kallade nano-ärtskidor. De senare är gjorda av ett nanorör fyllt av en kedja av fullerenmolekyler. Sådana modeller är baserade på en böjd kedja av sfärer anslutna med ledningar.

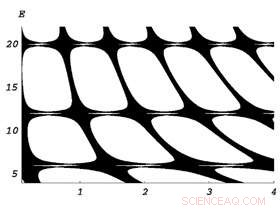
Forskarna beskrev sedan energispektrumet för system med störd periodicitet och gav sig i kast med att hitta villkoret för uppkomsten av lokala elektroner. Genom att använda en metod baserad på den så kallade allmänna teorin om operatorextension, de varierade längden på anslutningstrådarna, intensiteten av störningen och värdet på böjningsvinkeln.

Eremin och kollegor fann att lokaliserade elektroners utseende har ett starkare beroende av variationen av längden på trådarna i den böjda kedjan än variationen av värdet på böjningsvinkeln. Detta fynd överensstämmer med det faktum att en lokal störning inte påverkar det kontinuerliga spektrumet. När böjningsvinkeln tenderar mot noll, elektronerna tenderar att bli mindre lokaliserade.