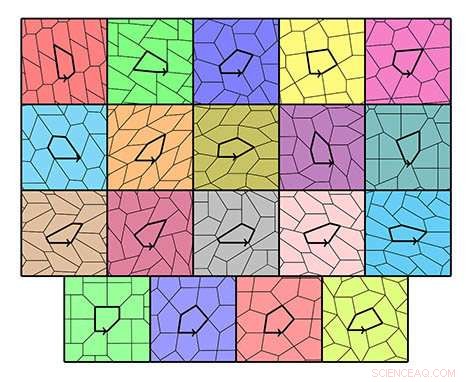
De 15 typerna av femkantiga plattor och deras 4 specifika typer © Michael Rao, Laboratoire d'informatique du parallélisme . Kredit:CNRS/Inria/ENS Lyon/Université Claude Bernard Lyon
Att kakla planet med ett enda mönster är ett matematiskt problem som har intresserat människor sedan antiken, särskilt för den estetiska kvaliteten på kakel i mosaik eller kakel. Ett av de olösta problemen inom detta område som har förbryllat vetenskapssamfundet sedan 1918 har nu definitivt lösts tack vare Michaël Rao från Laboratoire d'informatique du parallélisme (CNRS/Inria/ENS de Lyon/Université Claude Bernard Lyon 1). Med hjälp av datorverktyg kunde han visa att det bara finns 15 femsidiga mönster som kan belägga planet. Forskningen är nu tillgänglig på Arxiv hemsida.
Det finns ett antal lösningar för att täcka ett golv med en enda form, som trianglar, rutor, rektanglar, hexagoner, etc. Det uttömmande sökandet efter alla de konvexa former som kan belägga planet - en form med vinklar mindre än 180° som kan täcka en hel vägg utan att överlappa - initierades av Karl Reinhardt under sin avhandling 1918. Han visade att alla trianglar och fyrhörningar kan belägga planet, men att det bara fanns 3 typer av hexagoner som kunde göra det, och att en polygon med sju sidor eller fler inte kunde göra det. Endast frågan om femhörningar förblev öppen.
15 typer av femhörningar upptäcktes från 1918 till 2015 som en del av singulär forskning:initierad av Reinhardt 1918, det gick igenom ett antal vändningar, som nya upptäckter av amatörmatematiker, fram till det mediatiserade tillkännagivandet 2015 av en ny 15:e form 30 år efter den 14:e. Ändå kunde det vetenskapliga samfundet fortfarande inte avgöra om det fanns andra former av femhörningar som kunde kakla planet.
Michael Rao, en CNRS-forskare vid Laboratoire d'informatique du parallélisme (CNRS/Inria/ENS Lyon/Université Claude Bernard Lyon 1), har nu definitivt visat att det bara finns en ändlig serie av familjer av femhörningar att ta hänsyn till. Rao använde ett program för att generera alla möjligheter, och visade att 371 familjer av femhörningar potentiellt skulle kunna belägga planet. Han testade sedan var och en av dessa familjer med ett annat program, och visade att endast 19 typer av femhörningar uppfyllde villkoren för vinklar och sidolängder som krävs för att kakla planet. Bland dessa 19 typer, 15 motsvarade redan kända typer, och de fyra andra visade sig vara speciella fall av dessa 15 typer. Följaktligen, endast 15 typer av plattor kan kakla planet.
Rao kunde lösa ett hundraårigt problem med sin metodik, och öppna nya perspektiv. Alla dessa konvexa plattor kan belägga planet med jämna mellanrum (det vill säga brickorna upprepas i det oändliga). Ändå är det ännu inte känt om det finns en kakel som tillåter icke-periodisk plattsättning. Lyckligtvis kan de flesta av dessa tekniker också användas för icke-konvexa polygoner, och skulle därmed kunna tjäna som grund för att lösa ett annat problem inom plattsättningsområdet, mer känd som "Einstein-problemet" (från tyskans "ein stein").