
Tarski bevisade att en cirkel med en radie på ett inte helt kan täckas av remsor vars kombinerade bredd är mindre än två - cirkelns diameter. Var och en av remsorna i bilden har sin egen längd och färg. Kredit:MIPT
Israel Institute of Technology och Alexandr Polyanskii från Moscow Institute of Physics and Technology (MIPT) har bevisat László Fejes Tóths zonförmodan. Formulerad 1973, det står att om en enhetssfär är helt täckt av flera zoner, deras kombinerade bredd är minst π. Beviset, publiceras i tidskriften Geometrisk och funktionell analys , är viktig för diskret geometri och gör det möjligt för matematiker att formulera nya problem.
Diskret geometri studerar de kombinatoriska egenskaperna hos punkter, rader, cirklar, polygoner och andra geometriska objekt. Vilket är det största antalet lika stora bollar som får plats runt en annan boll av samma storlek? Vad är det tätaste sättet att packa lika stora cirklar i ett plan, eller bollar i ett utrymme? Dessa frågor och andra behandlas med diskret geometri.
Lösningar på problem som dessa har praktiska tillämpningar. Således, det täta packningsproblemet har hjälpt till att optimera kodningen och rätta till misstag vid dataöverföring. Ett ytterligare exempel är fyrfärgssatsen, som säger att fyra färger räcker för att rita någon karta på en sfär så att inga två angränsande regioner har samma färg. Det har fått matematiker att introducera begrepp som är viktiga för grafteorin, vilket är avgörande för många av den senaste utvecklingen inom kemi, biologi och datavetenskap, samt logistiksystem.
Tóths zonförmodan är nära besläktad med ett antal andra problem inom diskret geometri som löstes på 1900-talet som handlade om att täcka en yta med remsor. Det första bland dem var det så kallade plankproblemet, vilket innebar att täcka en skiva med remsor avgränsade av parallella linjer. Alfred Tarski och Henryk Moese gav ett enkelt bevis som visar att den kombinerade bredden på dessa remsor, eller plankor, kan inte överstiga skivans diameter. Det är, det finns inget bättre sätt att täcka en skiva än med en enda planka vars bredd är lika med skivans diameter. Thøger Bang löste sedan problemet med att täcka en godtycklig konvex kropp med remsor. Nämligen, han bevisade att den kombinerade bredden på remsorna som täcker en konvex kropp är åtminstone bredden på själva kroppen, det är, minsta bredd för en enda remsa som täcker kroppen.
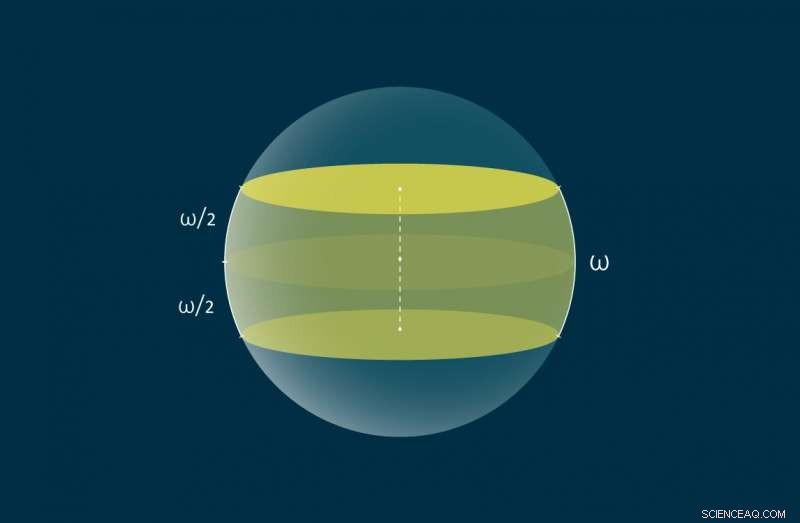
En zon med bredd ω på sfären visas i gult. Kredit:MIPT
Problemet som författarna tar upp är annorlunda genom att det handlar om att täcka en enhetssfär med speciellt konstruerade zoner. Specifikt, varje zon är skärningen av sfären med en viss tredimensionell planka, där en planka är rymdområdet mellan två parallella plan som är symmetriska med avseende på sfärens mitt. Alternativt zoner kan definieras i geodetiskt metriskt utrymme utan att använda plankor:En zon med bredd ω på ytan av en enhetssfär är den uppsättning punkter som inte ligger längre än ω/2 från storcirkeln, eller ekvator, med avstånden mellan punkterna mätt som de kortaste bågarna som förbinder dem. Matematikerna var tvungna att hitta den minsta kombinerade bredden av sådana zoner som täcker enhetssfären. Således, problemet skiljer sig från de tidigare lösta i hur bredd mäts - det definieras som längden på en båge, snarare än det euklidiska avståndet mellan parallella linjer eller plan.
Beviset från Jiang och Polyanskii inspirerades av Bang, vem löste problemet med att täcka en kropp med remsor genom att bilda en speciell ändlig uppsättning punkter i kroppen, varav den ena inte var täckt av någon av remsorna. På ett sätt, både Bang och författarna ger ett bevis genom motsägelse. När det gäller Fejes Tóths gissningar, matematikerna antog att den kombinerade bredden av zoner som helt täcker sfären var mindre än π och försökte komma fram till en motsägelse – nämligen, hitta en punkt som ligger på sfären men inte i någon av zonerna.
Författarna har visat att det är möjligt att bilda en uppsättning punkter i tredimensionellt utrymme så att åtminstone en punkt inte täcks av plankorna som utgör zonerna. Om hela denna uppsättning ligger inne i sfären, det är då relativt lätt att rita en annan punkt på sfären som inte heller täcks av plankorna, och därmed av zonerna. Om någon av punkterna i uppsättningen råkar ligga utanför sfären, det visar sig vara möjligt att ersätta en större zon med flera mindre, vars kombinerade bredd är lika med den större zonen. Således, det är möjligt att minska antalet zoner i det initiala problemet utan att påverka deras kombinerade bredd. Så småningom, en punkt på sfären identifieras som inte täcks av zonerna. Detta strider mot hypotesen att den kombinerade bredden av zonerna är mindre än π, bevisar Fejes Tóths gissning.

Zoner som helt täcker en sfär. Var och en av de fem zonerna har sin egen bredd och färg. Kredit:MIPT
Problemet löstes i n-dimensionell rymd, men författarna säger att detta inte skiljer sig från fallet med tre dimensioner.
"Fejes Tóths problem har fascinerat matematiker inom området diskret geometri i över 40 år, " säger författaren Alexandr Polyanskii vid Institutionen för diskret matematik, MIPT. "Det här problemet visade sig ha en elegant lösning, som vi hade turen att hitta. Fejes Tóths problem fick oss att överväga ett annat, mer grundläggande gissningar om täckningen av en sfär av förskjutna zoner definierade som skärningen av sfären med tredimensionella plankor som inte nödvändigtvis är centralt symmetriska."