Hur bevisar man något? Vad är ens bevis?

I vetenskap, ordet "bevis" används sällan och med stor försiktighet. Forskare accepterar att den naturliga världen är full av överraskningar, och det som verkar vara sant kan ha undantag.

I lagdomstolarna, bevis innehåller ofta en varning, såsom "om sannolikhetsavvägningen" för civilrättsliga frågor, och "utom rimligt tvivel" för brottmål.

Men till matematiker som University of Melbournes doktor Nick Beaton, Professor Jan de Gier och professor Tony Guttmann, "bortom rimligt tvivel" är helt enkelt inte tillräckligt bra. Till dem, ett matematiskt bevis är "utom allt tvivel" - och det är en sak av skönhet.

Tänk på Pythagoras sats.

Vi lär oss alla i skolan att kvadraten på den längsta sidan i en rätvinklig triangel är summan av kvadraterna på de två andra sidorna. Du kan testa detta med ett papper, en linjal och en miniräknare, och du kommer att se att det är sant.

Du kan göra detta för tusen trianglar och du kommer att se att det är sant för var och en av de tusen trianglarna.

Men fungerar Pythagoras sats för varje möjlig rätvinklig triangel?

Du kan inte mäta varje rätvinklig triangel som finns, så linjal- och kalkylatormetoden kan inte definitivt bevisa att Pythagoras har rätt.

"Du gör många simuleringar och du observerar en viss sak numeriskt, och om du observerar det om och om och om igen skulle du tro att det förmodligen alltid är fallet, eller det är sant, " säger Dr Nick Beaton.

"Men det är inte riktigt detsamma som att ha ett matematiskt bevis där man faktiskt logiskt kan visa att en viss sak alltid händer vid vissa värden på parametrarna."

Utan ett formellt matematiskt bevis, vi kallar något som Pythagoras sats en gissning.

Professor De Gier säger att en gissning i matematik är ett resultat som alla tror är sant.

"Men det har inte bevisats logiskt i en rigorös mening, " han säger.

"Så, det kan finnas många numeriska bevis och det kan finnas starka och övertygande argument, men de etablerar inte en sanning utom tvivel.

"Ett bra exempel är Riemann-hypotesen om zetafunktionens nollor, som har kontrollerats för de första 10, 000, 000, 000, 000 (tio biljoner) fall. Ett bevis på att det är sant för varje fall saknas fortfarande och är värt en miljon dollar, säger professor De Gier.

"Att bevisa det skulle kasta ljus över många av mysterierna kring fördelningen av primtal."

"Och ibland ser något väldigt övertygande ut men då visas det, när du borrar ner till de fina detaljerna, att det faktiskt inte håller och det kan finnas undantag."

Wikipedia har till och med en kategori för "motbevisade gissningar" – vissa, som Eulers gissning, stått i hundratals år innan de motbevisades.

När det gäller Pythagoras sats, dock, beviset har funnits med oss ​​i tusentals år. Faktiskt, Pythagoras uppfann inte formeln, det var känt långt före hans tid. Han kom med det första kända beviset.

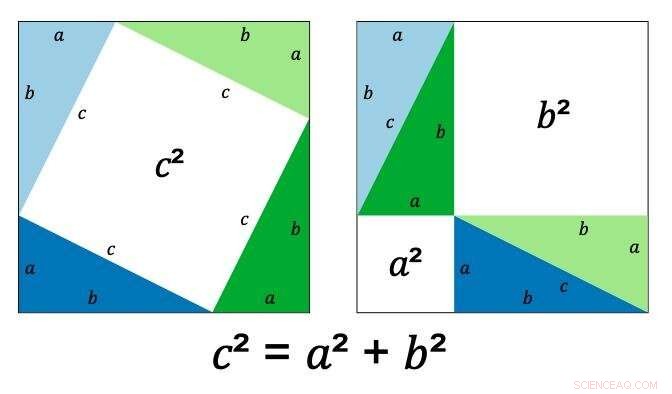
Pythagoras bevis använder det obestridliga faktum att vilken rätvinklig triangel som helst kan representeras av två kvadrater, den ena inuti den andra, med hörnen på den inre kvadraten vidrör kanten på den yttre.

Den inre kvadraten har sidor med längden c (den faktiska längden spelar ingen roll eftersom c kan vara vilket positivt tal som helst), den yttre kvadraten har längden a+b, och triangeln den gör har sidlängderna a, b och c (som visas).

Att ändra vinkeln på den inre kvadraten ändrar längden på alla tre värdena.

Pythagoras visade att genom att ordna om trianglarna inuti kvadraten, det vita området, representeras av c² i diagrammet ovan, blir två rutor, en med area a² och en med area b². Därav, c² är alltid, oavsett vilka mått du använder, lika med a²+b².

Sedan Pythagoras, matematiker genom tiderna har fortsatt att hitta bevis för satsen. 1940, Den amerikanske matematikern Elisha Scott Loomis publicerade en samling bevis för Pythagoras sats.

Teamet från University of Melbourne är inte främmande för bevis.

Australian Mathematical Society delade ut 2018 års Gavin Brown-pris för bästa uppsats till Dr Beaton, Professor de Gier och professor Guttman, tillsammans med Mireille Bousquet-Mélou från Université de Bordeaux i Frankrike och Hugo Duminil-Copin från Université de Genève i Schweiz, för ett matematiskt bevis 2015 på existensen och kritisk ytspänning för adsorption av polymerer (långkedjiga molekyler) i lösning.

Teamet använde en matematisk representation av en polymer, kallas en "självundvikande promenad, " som är föremål som används i en gren av matematisk fysik som kallas statistisk mekanik.

"En självundvikande promenad är en promenad på ett galler - ganska ofta ett fyrkantigt galler eller ett bikakegaller - där du inte kan spåra några av stegen du har tagit, " säger professor Guttmann.

"Du kan tänka på en promenad som en enda polymer, med slumpmässiga egenskaper."

Dr Beaton säger att ofta, att hitta ett matematiskt bevis för en gissning är en lång svår process, involverar trial-and-error, grymta arbete och en och annan eureka-ögonblick.

För Pythagoras, eureka-momentet var kvadrat-i-kvadrat-representationen av triangeln; för Melbourne-teamet och deras kollegor, det var att hitta det bästa sättet att matematiskt hantera slumpen.

"Folk försökte några saker när det först anades men ingen gjorde mycket framsteg, så det var tydligt att det behövdes en ny idé, men vad den nya idén skulle vara var inte självklart, säger professor De Gier.

Efter att ha följt några återvändsgränder, teamet fokuserade på en ny idé inom matematik förknippad med gittermodeller, kallad "diskret holomorficitet, " som populariserades av den ryske forskaren professor Stanislav Smirnov som vann Fields-medaljen för enastående upptäckter inom matematik 2010.

Genom att använda den här nya typen av matematik, teamet i Melbourne fann att bikakegittret var rätt inställning för att bevisa deras polymerproblem.

"Av någon anledning, matematiken för självundvikande promenader på ett bikakegaller fungerade bra, " säger professor de Gier.

"Om du vill göra detta på ett kvadratiskt galler, det fungerar inte, men för andra problem, det fyrkantiga gallret skulle vara bättre."

Professor de Gier säger att ett matematiskt bevis inte bara är en intellektuell övning, den kan berätta grundläggande saker om naturen.

"Att veta att något händer eller var det händer är av intresse, men att ha det logiska resonemanget är mer intressant eftersom det ger en inblick i varför saker händer som de gör."