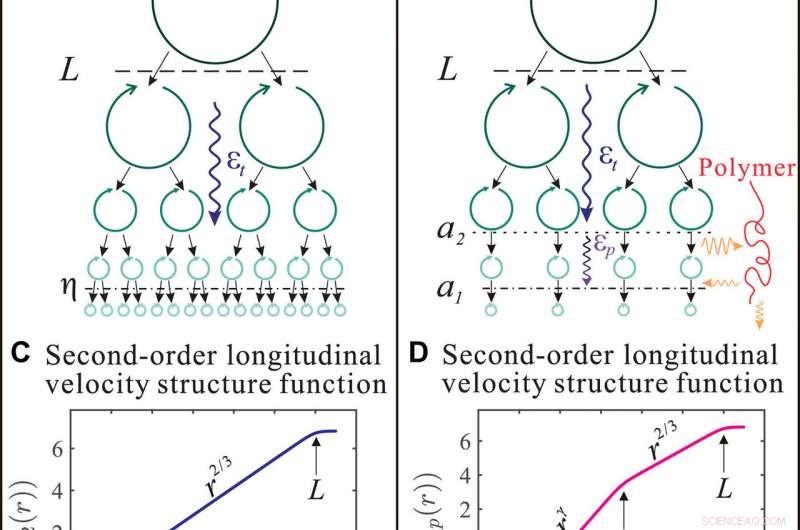
Fysisk bild av den turbulenta energikaskaden och dess manifestation på den andra ordningens longitudinella hastighetsstrukturfunktionen (VSF). (A och B) Teckningar som visar den fysiska bilden av energikaskaden i turbulent flöde av rent vatten och utspädd polymerlösning. (C och D) Andra ordningens longitudinella VSF i turbulent flöde av rent vatten och utspädd polymerlösning. Kredit:Science Advances, doi:10.1126/sciadv.abd3525
När långkedjiga flexibla polymerer löses i ett turbulent flöde, flödesegenskaperna kan ändras drastiskt genom att minska luftmotståndet och förbättra blandningen. En grundläggande gåta inom materialvetenskap är att förstå hur dessa polymertillsatser interagerar med olika rumsliga skalor i turbulent flöde för att förändra turbulensenergiöverföringen. I en ny rapport nu på Vetenskapens framsteg , Yi-Bao Zhang och en forskargrupp visade hur turbulent kinetisk energi kan överföras över olika skalor i närvaro av polymera tillsatser. Teamet noterade uppkomsten av ett tidigare oidentifierat skalområde känt som det elastiska området, där en ökad mängd energi kan överföras av polymerernas elasticitet. Fynden har viktiga tillämpningar i många turbulenta system, inklusive turbulens i plasma eller supervätskor.
Flödesegenskaper och hastighetsstrukturfunktion (VSF)
Materialforskare har visat hur upplösning av en liten mängd långkedjig flexibel polymer i en vätska kan förändra flödesegenskaperna. Reynolds nummer hjälper till att förutsäga flödesmönster under olika vätskeflödessituationer. På låga Reynolds, normalt vätskeflöde är stabilt och laminärt, och tillsatsen av polymerer kan inducera kraftiga fluktuationer för att skapa elastisk turbulens. Turbulenta flöden med högt Reynolds antal kan resultera i avsevärd minskning av motståndet och förbättring eller minskning av konvektiv värmeöverföring. Forskare strävar efter att förstå interaktionen mellan polymerer och turbulenskaskaden av teoretiska skäl och praktiska tillämpningar. Det är för närvarande kritiskt att heltäckande mäta energispektra eller hastighetsstrukturfunktionen (VSF) i turbulenta flöden med polymera tillsatser. I denna rapport, Zhang et al. detaljerade en experimentell observation av det nya elastiska området i en laboratorieturbulent flödesuppsättning och mätte skalningen av hastighetsstrukturfunktionen i det nya elastiska området, som avvek från alla existerande teorier.
Andra ordningens longitudinella VSFs [S2(r)] för rent vatten och utspädda polymerlösningar vid Rλ=530. (A) S2(r) och r är normaliserade med u2η och η, respektive. Här, Rλ, η, och uη är från fallet med rent vatten. De heldragna kurvorna passar till parametreringsfunktionen (Ekv. 2). För klarhets skull, lägre ϕ-data har flyttats uppåt med 100,15 med avseende på dess högre ϕ-granne. (B) Samma data som i (A) men S2, p(r) kompenseras av elastisk skalning r1,38. För klarhets skull, varje datauppsättning har flyttats upp med 0,25 med avseende på dess högre ϕ-granne. De cyan och magenta pentaklarna visar korsningsskalorna a1 mellan förlust- och elastiska intervall och a2 mellan elastiska och tröghetsintervall, respektive. (C) Samma data som i (A) men S2, p(r) kompenseras av sin exakta form i det elastiska området som ges av parametriseringen:s2xxa0.621r1.38, och r är normaliserad med a2. Den heldragna kurvan är (r/a2)−0,71. Kredit:Science Advances, doi:10.1126/sciadv.abd3525 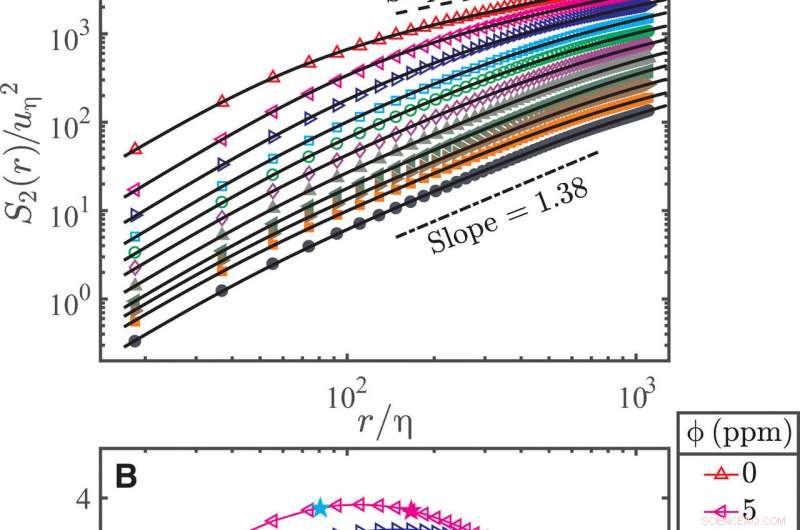
Forskarna genererade det turbulenta flödet i en von Kármán virvlande apparat som innehöll två motroterande skivor inneslutna i en cylindrisk tank fylld med 100 L vatten eller polymerlösningar. De mätte de tre komponenterna av vätskehastighet i en central plan som passerade genom tankens axel med hjälp av ett stereoskopiskt partikelbildshastighetssystem (PIV). Enligt måtten, flödet nära tankens mitt var nästan homogent och isotropt för både flöden med vatten och med utspädda lösningar av långkedjiga polymerer i vatten. Forskarna använde polyakrylamid (PAM) för polymererna under experimenten. Teamet noterade ett Reynolds-tal för det rena vattnet från 340 till 350, indikerar ett fullt utvecklat tröghetsintervall i turbulens. Vid jämvikt, polymererna förblev i lindat tillstånd. Under svagt flöde i lösningen, polymeren förblev i lindat tillstånd med försumbar effekt på flödet. Jämförelsevis, under intensivt flöde, polymererna sträcktes för att lagra elastisk energi för frisättning i vätskan. Vätskan visade sedan viskoelastiskt beteende. Under turbulenta flöden, de karakteriserade övergången med hjälp av Weissenberg-talet för att mäta polymerrelaxationstiden i förhållande till turbulenstidsskalan. För att polymererna ska sträckas av flödet, Weissenberg-talet måste vara större än enheten. Under mätningarna, Zhang et al. endast beaktade interaktionen mellan vätskan och enskild polymer, samtidigt som man försummar direkta polymer-polymer-interaktioner.
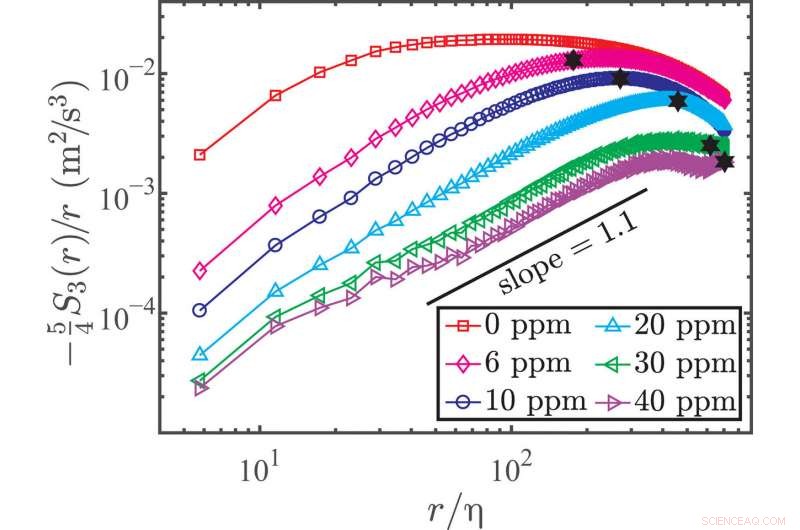
Den lokala turbulens kinetiska energiöverföringshastigheten bestämd från tredje ordningens longitudinella VSF. Kompenserad tredje ordningens longitudinella VSF −54S3(r)/r=ε(r) som en funktion av r/η för rent vattenfall och polymerlösningsfallen vid Rλ =480. De svarta pentaklarna visar korsningsskalan a2 mellan resåren och tröghetsintervallen. Kredit:Science Advances, doi:10.1126/sciadv.abd3525
Mätning av det elastiska området
För att sedan kvantifiera gränsen för det elastiska området, forskarna anpassade en analytisk form av andra ordningens longitudinella hastighetsstrukturfunktion (VSF) för Newtonsk turbulens föreslagen av Batchelor et al. När polymerkoncentrationen i provet ökade, den uppmätta medelkvadraten för derivatan av den longitudinella hastigheten minskade, vilket indikerar att energin som försvinner av viskositet i mycket små skalor - i överensstämmelse med tidigare experiment och numeriska simuleringar. Den minskade viskösa förlusten med polymerkoncentration tillsammans med oberoendet av turbulensenergiöverföringshastigheten vid större skalor indikerade att energiöverföringshastigheten i det elastiska området varierade icke-trivialt. Teamet undersökte därför metoder för att erhålla energiöverföringshastigheten med en uppsättning som drog inkrementellt mer energi in i polymerens elastiska energi på grund av interaktioner mellan turbulenta virvlar och polymerelasticitet.
Crossover-vågen.
Zhang et al. identifierade sedan det elastiska området och undersökte korsningsskalan mellan det elastiska området och förlustområdet (benämnt a1), följt av korsningsskalan mellan det elastiska området och tröghetsområdet (benämnt a2). De studerade sedan hur de två crossover-skalorna varierade med kontrollparametrar. Överkorsningsskalan mellan det elastiska området och förlustintervallet verkade minska något med polymerkoncentrationen; dock, teamet krediterade detta till trolig kontaminering på grund av dålig rumslig upplösning av partikelbildhastighetsmätningarna. Forskarna korrigerade sedan den observerade felaktigheten som en funktion av polymerkoncentrationen och visade att för små polymerkoncentrationer, korsningsskalan mellan det elastiska området och tröghetsområdet var mycket liten.
Variationen av korsningen skalar a1 mellan förlust- och elasticitetsområdena och a2 mellan elastiska och tröghetsområdena. a1 och a2 som funktioner av ϕ för fyra olika Rλ. Här, a1 och a2 är normaliserade med η från fallet med rent vatten. a1 vid lägre koncentration från tidigare experiment [Rλ =270, 340, 360 data från och Rλ =350 data från] plottas också för jämförelse. Lutningen =0,8 rät linje är för att visa att totalt a2 skalar med ϕ0,8, medan lutningen =0,4 rät linje är att jämföra data i det låga koncentrationsområdet med förutsägelsen rε ∼ ϕ0,4. 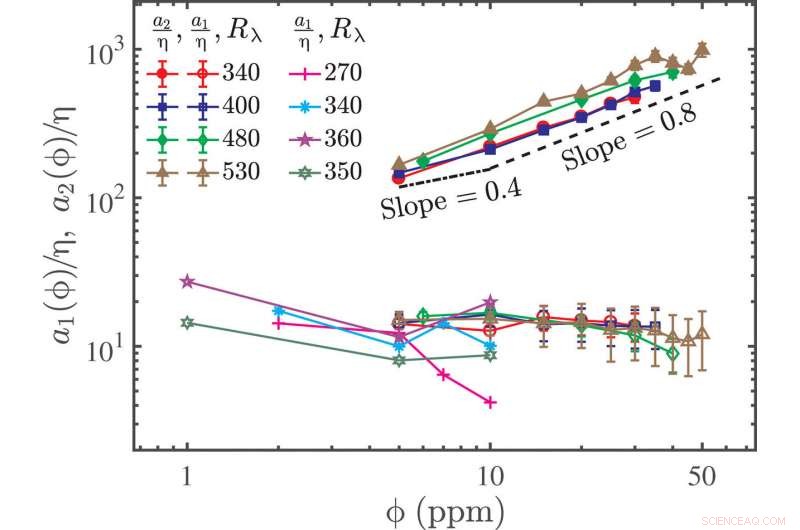
Teamet undersökte också problemet med turbulensflöde för att skala hög ordningens hastighetsstrukturfunktion (VSF) på tröghetsområdet med vatten och polymertillsatser. De resulterande likheterna i beteende visade hur det elastiska området för energiöverföringen genom skalor förändrades av polymerer. Teamet förväntar sig att observera gemensamma drag mellan Newtons turbulens och polymer turbulens. Resultaten visade utmärkt överensstämmelse mellan data och förutsägelse för att visa hur energiöverföringen väsentligt förändrades av polymerer i det elastiska området. Under tiden följde den fluktuerande lokala energiöverföringen liknande statistiska beskrivningar som den för Newtonsk turbulens.
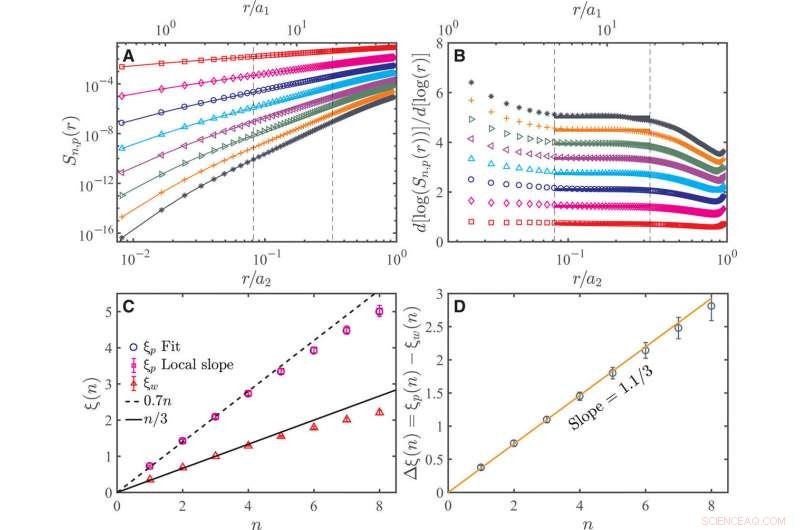
Skalning av VSF av hög ordning i det elastiska området vid Rλ=480 och ϕ=40 ppm. (A) N:te ordningen (n=1 till 8, från topp till botten) longitudinell VSF i polymerlösningen Sn, p(r) som en funktion av r/a2 (eller r/a1, övre axeln), intervallet mellan de två vertikala streckade linjerna är det elastiska intervallet, skalningsexponenten ξp(n) erhålls från effektlagens anpassning till detta område. De absoluta värdena för hastighetsökningarna används för att beräkna VSF. (B) Lokal lutning d[ log (Sn, p(r))]/d[ log (r)] av Sn, p(r) för n=1 till 8 (från botten till toppen) som en funktion av r/a2 (eller r/a1, övre axeln). De två vertikala streckade linjerna markerar området där den lokala lutningen är nästan konstant. De horisontella heldragna linjerna representerar medelvärdet inom de två streckade linjerna. (C) Elastiska skalningsexponenter ξp som funktion av n. ξp erhållen från både den direkta passningen och den lokala lutningen plottas. Skalningsexponenterna för tröghetsintervallet för rent vatten ξw(n) plottas också för jämförelse. Den streckade linjen är ξp(n) =0,7n. Den heldragna linjen är K41-förutsägelsen, dvs. ξw(n) =n/3. (D) Δξ(n) =ξp(n) − ξw(n) som en funktion av n. Den heldragna linjen är Δξ(n) =1,1n/3.
Syn
På det här sättet, Yi-Bao Zhang och kollegor observerade experimentellt skalningen av det elastiska området i det turbulenta flödet med polymertillsatser. De mätte den turbulenta kinetiska energiöverföringen i närvaro av polymera tillsatser. När energiflödet genom det turbulenta flödet minskade, energiflödet genom polymerernas elastiska frihetsgrad ökade. Studien kastade nytt ljus för att genomföra ytterligare teoretiska och numeriska undersökningar av interaktionen mellan elasticiteten hos polymertillsatser och turbulenta virvlar. Dessa experimentella processer kan noteras i praktiken inom fysikaliska mekanismer som elektromagnetiska interaktioner i plasma och Alfvén-vågor i superfluids.
© 2021 Science X Network