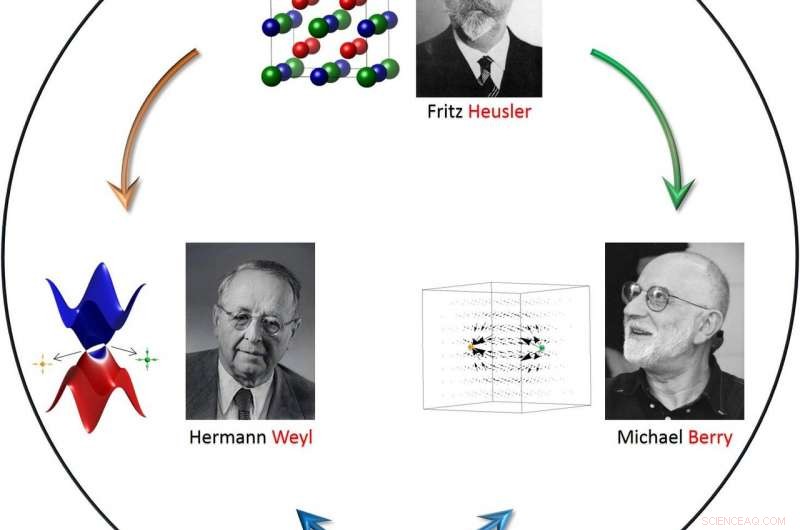
Figuren visar sambandet mellan Weyl fermioner och Berry -fasen och dess förverkligande i Heusler -familjen av föreningar. I den övre panelen, vi presenterar ett typiskt atomarrangemang för en hel-Heusler-legering där de röda och blå sfärerna är övergångsmetaller (som kobolt eller järn), med rött som är mer elektropositivt än blått, och den gröna sfären är ett huvudgruppselement (som kisel eller Gallium). I den nedre panelen, den elektroniska strukturen för Weyl halvmetal visas. De gula och ljusgröna punkterna presenterar de magnetiska monopolerna i en kiral Weyl -halvmetal och de svarta pilarna anger Berry -krökning i momentumutrymmet. Kredit:Heusler:Isabellenhütte GmbH &Co. KG; Weyl:ETH Zürich Bildarchiv; Berry:Michael Berry
Forskare vid Max Planck Institute Chemical Physics of Solids har skrivit en granskningsrapport om magnetiska topologiska material i familjen Heusler -föreningar. Granskningen förklarar sambandet mellan topologi, symmetri och magnetism på en nivå som är lämplig för studenter i fysik, kemi och materialvetenskap med en grundläggande kunskap om fysik i kondenserad materia.
Fritz Heusler (1866-1947), Hermann Weyl (1885-1955) och Michael Berry (1941-) är tre kända forskare vars arbete har lett till nya och viktiga insikter i materialvetenskap, topologi och kondensfysik. Dessa tre vetenskapsområden har kommit ihop nyligen med upptäckten av nya och spännande kvantegenskaper i nya materialklasser som kan möjliggöra ny vetenskap inklusive datorteknik och katalys.
Heusler är namnet på upptäckaren av mestadels magnetiska föreningar som var av intresse för ganska länge sedan. Men dessa föreningar visade sig nyligen vara värd för icke-triviala topologiska egenskaper som öppnar ett stort område inom ny fysik. Dolda i energibandstrukturen för dessa material finns enstaka punkter som kan beskrivas med matematiska verktyg som härstammar från Weyl; dessa punkter är associerade med upptäckten av kvasipartiklar som nu kallas Weyl fermioner. De finns inte bland de elementära partiklarna i högenergifysik, men vi tror att de existerar i fasta material och bestämmer deras topologi. Det tredje namnet Berry står för de mätbara effekterna som avslöjar fysiken till hands. Under vissa väldefinierade förhållanden finns det ett vektorfält, liknar magnetfältet, kallade Berry -krökning. Det bestämmer storleken på ett antal viktiga effekter, såsom den avvikande Hall -effekten och Spin Hall -effekten. Det är experimentens konst att på ett lämpligt sätt modifiera materialen för att ställa in Berry -krökning och därmed göra topologin synlig. I denna recension ges ett stort antal exempel på olika symmetriegenskaper hos Heusler -föreningar, en stor klass av material som enkelt kan ställas in för att visa ferromagnetisk, antiferromagnetisk, icke-kollinjär eller kompenserad magnetisk ordning. Dessa magnetiska ordningar ger upphov till uttalade elektriska och termoelektriska effekter vars fingeravtryck avslöjas och förklaras inklusive partikelliknande virvelspinnstrukturer, antiskyrmionerna som är typiska för en viss delmängd av Heusler -föreningar.
Med tanke på det stora antalet befintliga oorganiska föreningar och det nyligen föreslagna stora antalet icke -magnetiska topologiska material, Heusler -föreningar fungerar som ett modellsystem för förståelse och påverkan av magnetism på topologi. Brytningstidssymmetri via magnetism eller ett externt magnetfält kan leda till ännu större effekter än i icke-magnetiska material baserat på den stora skillnaden mellan Weyl-punkter i olika kiraliteter. Baserat på en systematisk studie av Heusler -material förutspår vi att det finns ett stort antal magnetiska topologiska material som väntar på att upptäckas.
När det gäller ansökningar, den stora Nernst -effekten och klassiska och kvante Hall -effekter runt rumstemperatur baserat på de höga Curie -temperaturerna hos Heusler -föreningar och deras släktingar har potential att ha stor inverkan på energiomvandling och kvantelektroniska apparater för spintronik eller kvantberäkning.