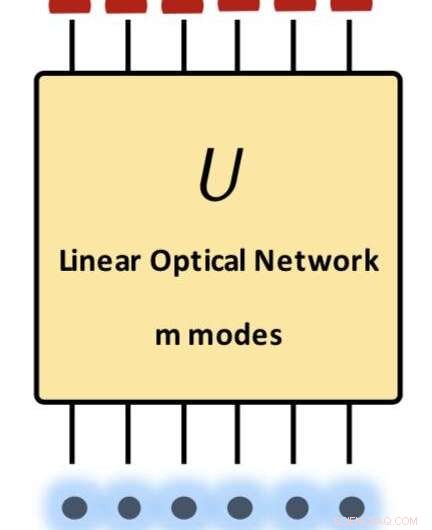
Sammanfattning av vårt huvudresultat:en övre gräns för övergångsamplituderna för linjär optik. De initiala och slutliga tillstånden är produkter av Fock-tillstånd. Matrisen U presenterar varje realiserbar enhetlig transformation i linjär optik. Kredit:Science China Press
Linjär optik utgör ett av de bästa exemplen för att demonstrera kvantfysik. Det fungerar i rumstemperatur, och kan observeras med relativt enkla anordningar. Linjär optik involverar fysiska processer som bevarar det totala antalet fotoner. I det ideala fallet, om det finns 100 fotoner i början, oavsett hur komplicerad den fysiska processen är, det kommer att finnas exakt 100 fotoner kvar till slut.
Fotoner är bosoniska icke-interagerande partiklar. Dock, de kan fortfarande störa varandra, uppvisar icke-triviala kvanteffekter. Ett typiskt exempel är Hong-Ou-Mandel-experimentet, där två identiska fotoner skickas till en experimentell enhet. Efter en enkel linjär transformation, de två fotonerna verkar som om de sitter ihop och ovilliga att separera. Förutom att ge en grundläggande förståelse för kvantmekanik, studiet av linjär optik har också lett till många vetenskapliga tillämpningar.
Under de senaste åren har de unika egenskaperna hos linjära optiska system har också inspirerat utvecklingen av beräkningskomplexitetsteori. Under 2012, Professor Scott Aaronson vid MIT (för närvarande vid University of Texas i Austin) föreslog en linjär optisk metod för att demonstrera kvantöverlägsenhet (beräkning) som bygger på konceptet bosonprovtagning. Mer specifikt, Aaronson föreslog att för en klass av provtagningsproblem baserade på linjära optiska system, det skulle vara omöjligt i praktiken att använda någon klassisk dator för att simulera. Denna idé startar omedelbart en kapplöpning för att nå statusen "kvantöverhöghet". Många kvantoptiska laboratorier runt om i världen har blivit intresserade av att utveckla bosonsamplingssystem för att slå rekord när det gäller fotonantal. Å andra sidan, datavetare är upptagna med att använda superdatorer för att höja ribban för att uppnå kvantöverlägsenhet.
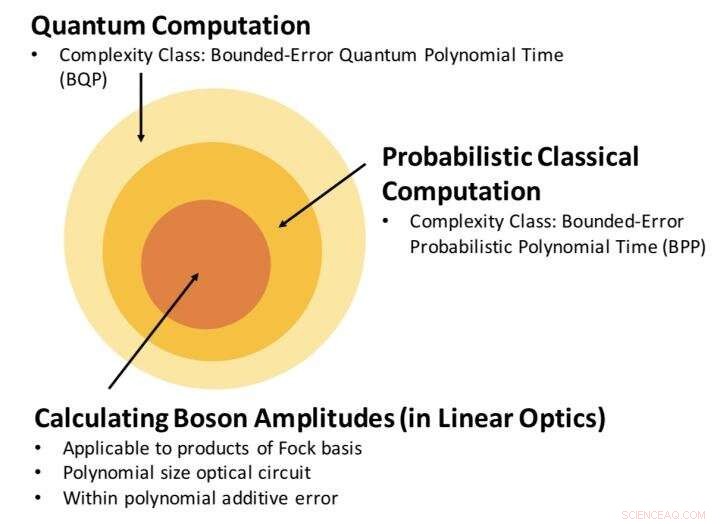
Förhållandet mellan av komplexitetsklassen för att uppskatta bosonamplitud, och klassisk och kvantberäkning. Vårt resultat fastställer att beräkning av bosonamplituden, med ett polynom additivt fel, är ett problem inom BPP. Kredit:Science China Press
Dock, när det gäller praktiska problem, att tillämpa modellen för bosonprovtagning är inte ett bra tillvägagångssätt. Därför, Aaronson ställde en fråga 2012:Förutom provtagningsproblem, kan forskare utnyttja linjär optik för att uppnå kvantöverlägsenhet när det gäller beslutsproblem med ett JA/NEJ-svar? Nyligen, Prof. Man-Hong Yung, docent i SUSTech och hans kollegor publicerade en artikel med titeln "Universal bound on sampling bosons in linear optics and its computational implications" i National Science Review ( NSR ), erbjuder en komplett lösning på det öppna problem som Aaronson ställer.
Specifikt, Yungs team upptäckte en grundläggande gräns för övergångssannolikheterna för linjära optiska system, begränsar förmågan att överföra bosoner med linjära optiska enheter. Tillsammans med kvantoptikens verktyg, de utvecklade en klassisk algoritm som effektivt kan uppskatta övergångsamplituden med ett begränsat fel. Följaktligen, dessa resultat leder till ett negativt svar på Aaronsons öppna problem. Med andra ord, för kodning av svåra beslutsproblem, det är nödvändigt att använda mer komplicerade kvantoptiksystem istället för bara linjär optik.
Som en tvärvetenskaplig domän mellan kvantfysik och datavetenskap, kvantinformationsvetenskap är fortfarande ett mycket aktivt forskningsområde. Å ena sidan, resultaten av Yungs team bidrar till den teoretiska grunden för kvantoptik; å andra sidan, förutom bosonprovtagning, dessa resultat pekar på ett nytt perspektiv på beräkningskomplexitetsproblem i termer av kvantoptik. Otvivelaktigt, i framtiden, vi bör förvänta oss att se många fler spännande resultat som dessa på detta område.