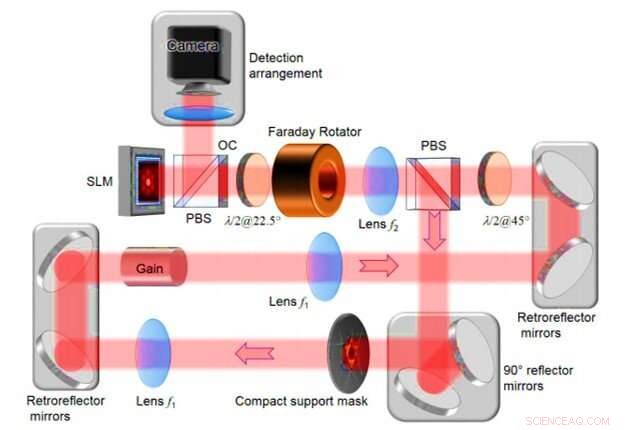
Detaljerat experimentellt arrangemang för digital ring degenererad kavitetslaser. SLM - rumslig ljusmodulator; PBS - polariserande stråldelare; λ/2@22,5° - halvvågsplatta vid 22,5° vinkelorientering; λ/2@45° - halvvågsplatta vid 45° vinkelorientering; kompakt stödmask - intrakavitetsöppning vid Fourierplanet; OC–utgångskoppling. Upphovsman:Science Advances, doi:10.1126/sciadv.aax4530
Fysiker kan utforska skräddarsydda fysiska system för att snabbt lösa utmanande beräkningsuppgifter genom att utveckla spinsimulatorer, kombinatorisk optimering och fokusering av ljus genom spridningsmedia. I en ny rapport om Vetenskapliga framsteg , C. Tradonsky och en grupp forskare vid avdelningarna för fysik i Israel och Indien behandlade fashämtningsproblemet genom att rekonstruera ett objekt från dess spridda intensitetsfördelning. Den experimentella processen tog upp ett existerande problem inom discipliner som sträcker sig från röntgenbilder till astrofysik som saknar tekniker för att rekonstruera ett objekt av intresse, där forskare vanligtvis använder indirekta iterativa algoritmer som är långsamma.
I det nya optiska tillvägagångssättet, Tradonsky et al använde omvänt ett DDCL-läge (digital degenerate cavity laser) för att snabbt och effektivt rekonstruera föremålet av intresse. De experimentella resultaten antydde att vinstkonkurrensen mellan de många lasrlägena fungerade som en mycket parallell dator för att snabbt lösa fasåtervinningsproblemet. Tillvägagångssättet gäller tvådimensionella (2-D) objekt med känt kompakt stöd och komplext värderade objekt, att generalisera bildåtergivning genom spridningsmedia, samtidigt som du utför andra utmanande beräkningsuppgifter.
För att relativt enkelt beräkna intensitetsfördelningen av ljus spritt långt från ett okänt föremål, forskare kan beräkna källan till det absoluta värdet av ett objekts Fouriertransform. Rekonstruktionen av ett objekt från dess spridda intensitetsfördelning är, dock, illa ställd, eftersom fasinformation kan gå förlorad och olika fasfördelningar i arbetet kan resultera i olika rekonstruktioner. Forskare måste därför skaffa tidigare information om ett föremåls form, positivitet, rumslig symmetri eller sparsitet för mer exakta objektrekonstruktioner. Sådana exempel finns inom astronomi, kortpulskarakteriseringsstudier, Röntgendiffraktion, radardetektering, taligenkänning och vid bildtagning över grumliga medier. Under rekonstruktionen av föremål med en ändlig utsträckning (kompakt stöd), forskare erbjuder en unik lösning på fashämtningsproblemet, så länge de modellerar samma spridda intensitet vid en tillräckligt högre upplösning.
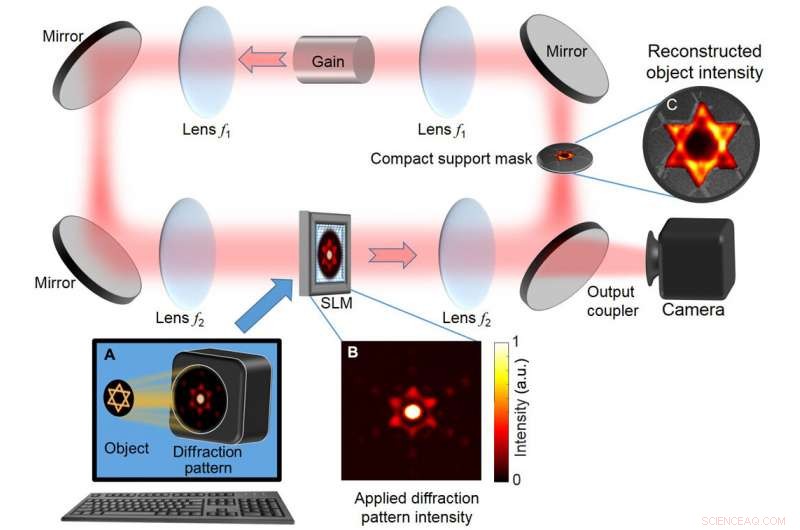
Grundläggande DDCL-arrangemang för snabb fasåtervinning. (A) Beräknad spridd intensitetsfördelning från objektet (i huvudsak Fourierintensitetsfördelningen) appliceras på en SLM, som är inkorporerad i en ring degenererad kavitetslaser som kan stödja upp till 100, 000 degenererade tvärlägen. En mask formad som objektgränserna (kompakt stöd) vid Fourierplanet filtrerar bort främmande lägen som inte matchar det kompakta stödet. Med detta laserarrangemang, lasringsprocessen ger en självständig lösning som uppfyller både den spridda intensitetsfördelningen som visas i (B) och den kompakta stödbegränsningen. (C) Den rekonstruerade objektintensiteten visas vid den kompakta stödmasken och avbildas på kameran. a.u., godtyckliga enheter. Upphovsman:Science Advances, doi:10.1126/sciadv.aax4530
Fysiker hade utvecklat flera algoritmer för att lösa fasåtervinningsproblemet under det senaste decenniet, inklusive Gerchberg-Saxton (GS) felreduktionsalgoritm, hybrid input-input-algoritm och avslappnad medelvärde för alternerande reflektioner (RAAR). Dock, de är baserade på iterativa projektioner som är relativt långsamma även på högpresterande datorer. Som ett alternativ, forskarlag kan ta itu med beräkningsutmaningar med hjälp av specifikt skräddarsydda fysiska system. Även om sådana system inte är universella Turing-maskiner (dvs. de kan inte utföra godtyckliga beräkningar), de kan potentiellt lösa en specifik klass av problem effektivt. Att lösa svåra problem med sådana system kan vara fördelaktigt jämfört med användningen av konventionella datorer.
Tradonsky et al demonstrerade experimentellt ett nytt optiskt system för att snabbt lösa fasåtervinningsproblem baserat på en digital degenererad kavitetslaser (DDCL). Enheten inkorporerade två begränsningar, inklusive Fourier-storlekarna av spritt ljus från ett föremål och det kompakta stödet. Den olinjära laserprocessen i kaviteten resulterade i en självständig lösning som tillfredsställde båda begränsningarna. Den bakomliggande fysiska mekanismen i DDCL var liknande den som observerades med optiska parametriska oscillator (OPO) spin -stimulatorer.
Både OPO-simulatorer och DDCL:er har utfört optimeringar via extremt snabb drift med möjlighet att undvika lokala minima och innehade ett icke-Gaussiskt vågpaket. Forskarna underlättade den kompakta stödöppningen i kaviteten för att säkerställa olika konfigurationer av laserfaser för att resultera i olika förluster, för att tillåta konfigurationen med minimala förluster för att vinna lägestävlingen och lösa fasproblemet. DDCL -systemet innehöll många attraktiva och viktiga funktioner, inklusive hög parallellitet för att ge miljontals parallella experimentella insikter, korta rundturstider på ungefär 20 nanosekunder, snabba konvergenstider och ett inneboende urvalsläge som stod för minimal förlust på grund av modkonkurrens. I teorin, av alla tidsutvecklande faskonfigurationer, den med högst energi vann lägestävlingen i förhållande till den begränsade vinsten. Som ett resultat, större antalet initiala oberoende konfigurationer i praktiken, högre sannolikhet för systemet att hitta en korrekt lösning med en stabil konfiguration och inga förluster.
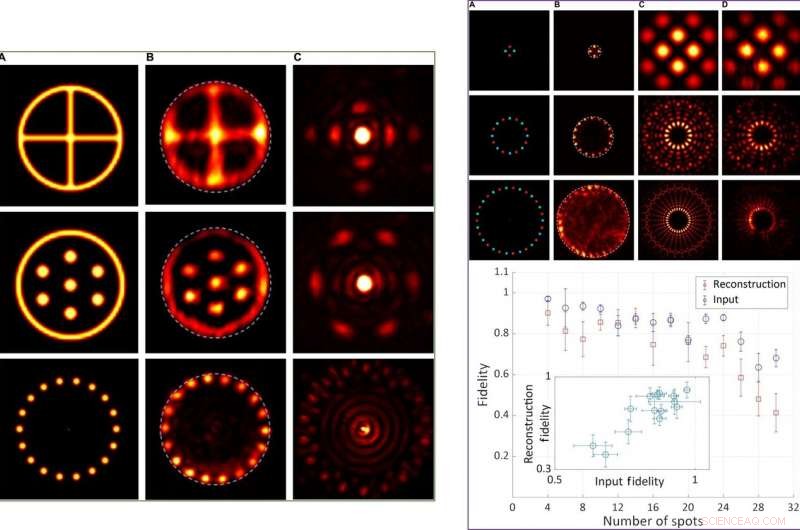
VÄNSTER:Experimentella resultat för verkligt värderade centrosymmetriska objekt. Kolumn (A) Intensitetsfördelningar av de faktiska objekten. Kolumn (B) Detekterad intensitetsfördelning av de rekonstruerade objekten, använda en cirkulär öppning som kompakt stöd. Kolumn (C) Fourierintensitetsfördelningar vid SLM. HÖGER:Experimentella och kvantitativa resultat för trohet som funktion av objektets komplexitet. Överst:Representativa intensitetsfördelningar av objekt med 4, 16, och 30 platser. Kolumn (A) Fördelningar av intensitet (ljusstyrka) och fas (nyans) för de faktiska objekten. Kolumn (B) Detekterad intensitetsfördelning av de rekonstruerade objekten, använda en cirkulär öppning som kompakt stöd. Kolumn (C) Beräknade Fourier-intensitetsfördelningar som tillämpas för att styra SLM. Kolumn (D) Detekterade motsvarande Fourier-intensitetsfördelningar efter modifieringar av SLM-egenskaper. Nederst:Kvantitativa trohetsvärden för Fourierintensitetsfördelningarna (blå) och de rekonstruerade objektintensitetsfördelningarna (röda) som en funktion av antalet fläckar i objektet (4 till 30). Insättning:Fidelitetsvärden för de rekonstruerade objektintensitetsfördelningarna som en funktion av trohetsvärdena för Fourierintensitetsfördelningarna för alla mätningar. Upphovsman:Science Advances, doi:10.1126/sciadv.aax4530.
I den experimentella inställningen, Tradonsky et al inkluderade en ringdegenererad kavitetslaser med ett inneboende förstärkningsmedium, två 4f-teleskop och en amplitud spatial ljusmodulator (SLM). Systemet inkluderade också en intrakavitetsöppning, 3D-reflekterande speglar och en utgångskopplare. Teamet använde de vänstra 4f-teleskopen för att avbilda mitten av förstärkningsmediet på SLM och kontrollerade överföringen vid varje pixel, oberoende av. De kombinerade intrakavitetsöppningen med SLM för att kontrollera och bilda utmatningslaserintensitetsfördelningen. När forskarna placerade en intrakavitetsöppning (kompakt stödmask) vid Fourierplanet mellan de två linserna, varje fasfördelning visade en annan nivå av förlust. Följaktligen, fasfördelningen med minimal förlust var det mest sannolika lasermodet i studien. Teamet övervägde två värdesiffror för att kvantifiera kvaliteten på systemet, inklusive lösningstrohet och beräkningstid. Forskargruppen erhöll representativa resultat för centrosymmetriska objekt med mycket god överensstämmelse mellan intensitetsfördelningar av det ursprungliga (faktiska objektet) och rekonstruerade former.
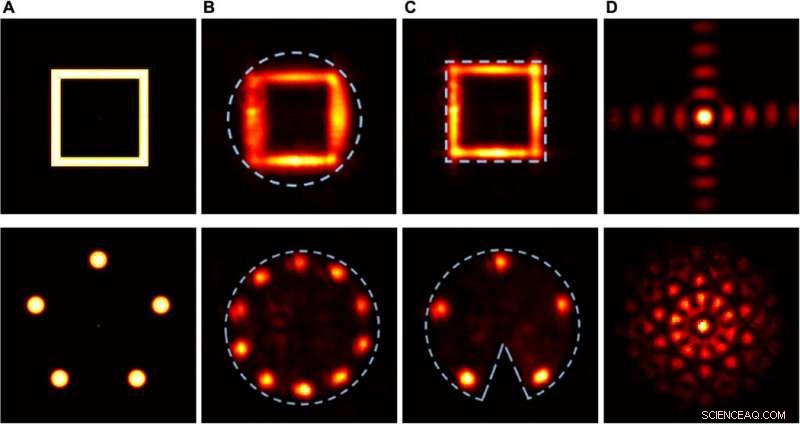
Experimentella resultat som visar den kvalitativa effekten av täthet och asymmetri hos kompakta stöd. Kolumn (A) Intensitetsfördelning av de faktiska objekten. Kolumn (B) Detekterad intensitetsfördelning av de rekonstruerade objekten, använda en cirkulär öppning som kompakt stöd. Kolumn (C) Detekterad intensitetsfördelning av de rekonstruerade objekten, med en fyrkantig bländare som tätt kompakt stöd (övre raden) och en cirkulär bländare med en kil som asymmetrisk kompakt stöd (nedre raden). Kolumn (D) Fourierintensitetsfördelningar vid SLM. Upphovsman:Science Advances, doi:10.1126/sciadv.aax4530
Tradonsky et al mätte effekten av objektkomplexitet på rekonstruktionstrohet och bildade representativa intensitetsfördelningar för objekt med fyra, 16, och 30 platser. Resultaten visade att objekt med högre komplexitet (de med fler fläckar) visade Fourierintensitetsfördelning med högre komplexitet, med invecklade detaljer som inte kunde lösas med det nuvarande systemet. De noterade också att indata och rekonstruktionstrohet minskar med ökande objektkomplexitet, vilket de krediterade det fluktuerande tekniska bullret från laserpumpen. De genomförde kvalitativa experiment för att bedöma effekten av täthet och symmetri under objektrekonstruktion. Resultaten visade att ett tätt kompakt stöd avsevärt förbättrade kvaliteten på det rekonstruerade objektet.
Teamet undersökte sedan de kvantitativa effekterna av radien hos den kompakta stödöppningen på kvaliteten och trovärdigheten vid återuppbyggnad. För större föremål genomgick den representativa intensiteten snabbt förfall under rekonstruktionstrohet eftersom lasern inte kunde stödja föremålets form. Med föremål som är mindre än den kompakta stödöppningen, Tradonsky et al observerade långsammare förfall i trohet. Totalt, de observerade minskad rekonstruktionstrohet när kameran tog ett medelvärde över flera realiseringar av ett objekt i systemet.
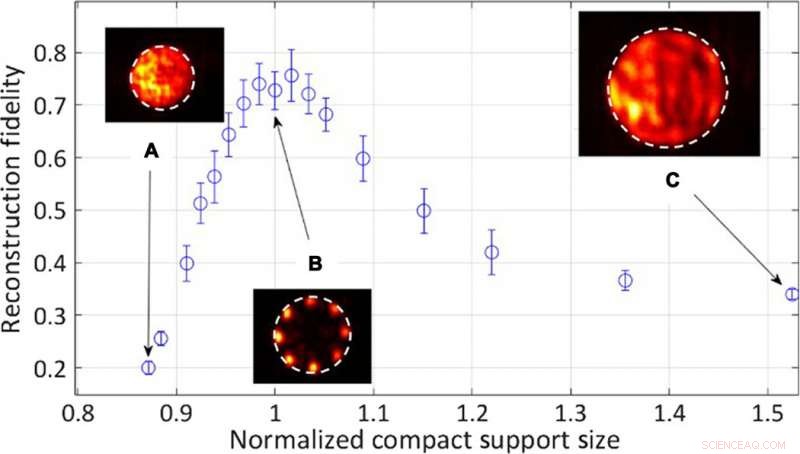
Experimentella kvantitativa resultat för rekonstruktionstrohet som en funktion av den kompakta stödradien för öppningen normaliserad av objektstorleken. Insättningar:Typiska rekonstruerade objektintensitetsfördelningar. (A) Kompakt stödradie är 87 % av objektradien. (B) Objektradien är lika med den kompakta stödradien. (C) Kompakt stödradie är 152 % av objektradien. Upphovsman:Science Advances, doi:10.1126/sciadv.aax4530.
Rent generellt, upplösningen av de rekonstruerade objekten var relativt låg på grund av fasavvikelser i laserkaviteten. Teamet föreslog att optimera systemet och minska avvikelser för förbättrad upplösning. Forskarna analyserade också den tid det tog att erbjuda en rekonstruktionslösning med hjälp av systemet och fann att varaktigheterna dikterade av SLM (spatial light modulator) och kameraavläsningen till ungefär 20 ms. Den faktiska beräkningstiden för lasring varade bara mindre än 100 nanosekunder. När Tradonsky et al optimerade experimentuppställningen med hjälp av ett Q-switchat linjärt degenererat hålrumslaserarrangemang med pockelceller, de minskade den totala beräkningstiden för systemet till cirka 100 nanosekunder. Jämförelsevis, rekonstruktionstiden med RAAR-algoritmen varade en sekund.
På det här sättet. C. Tradonsky och kollegor presenterade ett optiskt system för snabb fasåtervinning med hjälp av en ny DDCL (digital degenerated cavity laser). Beräkningstiden uppgick till 100 nanosekunder; storleksordningar snabbare än konventionella, algoritmbaserade beräkningssystem. Baserat på resultaten, flera modifieringar av DDCL-systemet kan potentiellt förbättra dess prestanda, inklusive ökad längd av laserhåligheten för att öka antalet oberoende parallella undersökningar. Forskargruppen kommer att ytterligare utforska systemet för att lösa en mängd olika problem och lösa bildkvalitet efter spridning genom spridningsmedia.
© 2019 Science X Network