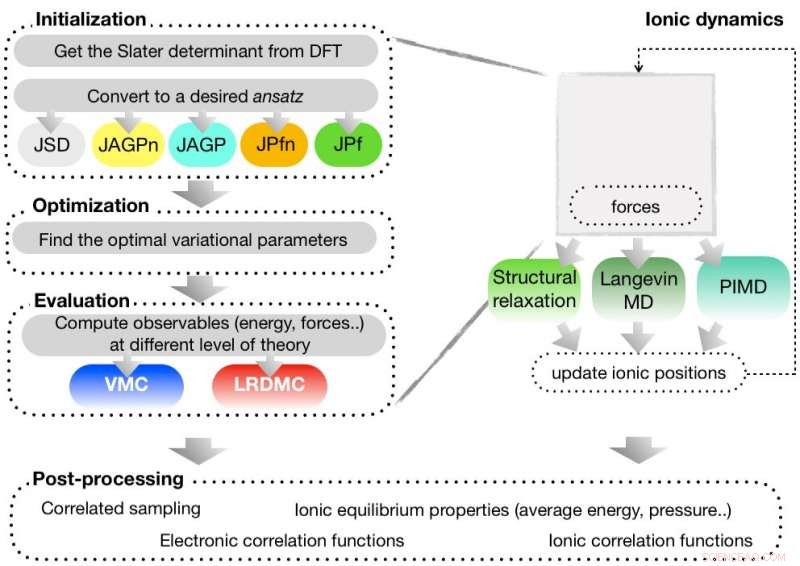
Schematisk bild av TurboRVB-arbetsflödet [K. Nakano et al. J. Chem. Phys. 152, 204121 (2020)]. Koden implementerar flexibel mångkroppsvågsfunktion ansatz, som JSD:Jastrow Slater, JAGP:Jastrow Geminal, och JPf:Jastrow Pfaffian. Man kan förbereda en provvågsfunktion med hjälp av en inbyggd densitetsfunktionsteori (DFT)-kod och utföra efterföljande första principer för variationskvantum Monte Carlo (VMC) och gitterdiskretiserade diffusionskvant Monte Carlo (LRDMC) beräkningar. Eftersom krafter som verkar på atomer kan beräknas, strukturella optimeringar och simuleringar av molekylär dynamik är också möjliga i TurboRVB. Upphovsman:AIP Publishing
First-principles quantum Monte Carlo är ett ramverk som används för att tackla lösningen av Schrödinger-ekvationen med många kroppar med hjälp av ett stokastiskt tillvägagångssätt. Detta ramverk förväntas bli nästa generation av elektroniska strukturberäkningar eftersom det kan övervinna några av nackdelarna i densitetsfunktionsteori och vågfunktionsbaserade beräkningar. Särskilt, Monte Carlo-kvantramverket förlitar sig inte på utbyteskorrelationsfunktioner, Algoritmen är väl lämpad för massivt parallella superdatorer, och det är lätt att applicera på både isolerade och periodiska system.
TurboRVB är ett kvant-Monte Carlo-mjukvarupaket med första principer som ursprungligen lanserades av Prof. Sandro Sorella (International School for Advanced Studies/Italien) och Dr. Michele Casula (Sorbonne University/Frankrike), och har kontinuerligt utvecklats av många bidragsgivare i över 20 år. Väldigt nyligen, Hjälpa. Prof. Kosuke Nakano vid Japan Advanced Institute of Science and Technology (JAIST, Ordförande:Minoru Terano, ligger på Nomi, Ishikawa, Japan) och hans medarbetare har publicerat en omfattande recensionsartikel i Journal of Chemical Physics .
TurboRVB kan särskiljas från andra första principer kvant Monte Carlo-koder i följande funktioner. (a) Koden använder vågfunktioner av typen resonerande valensbindning (RVB), som Jastrow Geminal/Jastrow Pfaffian, som inkluderar korrelationseffekten bortom Jastrow-Slater-vågfunktionen som vanligtvis används i andra QMC-koder. (b) Den implementerar toppmoderna optimeringsalgoritmer, såsom den stokastiska omkonfigurationen och den linjära metoden, hjälper till att realisera en stabil optimering av amplituden och nodytan för en vågfunktion med många kroppar på den variationsmässiga kvantmängden Monte Carlo-nivån. (c) Den så kallade lattice-regularized diffusion Monte Carlo-metoden är implementerad i koden, vilket ger en numeriskt stabil diffusionskvant Monte Carlo-beräkning. (d) Genomförandet av en angränsande algoritmisk differentiering gör att vi kan beräkna derivat av många kroppsvågsfunktioner mycket effektivt och utföra strukturoptimeringar och molekylära dynamiksimuleringar.