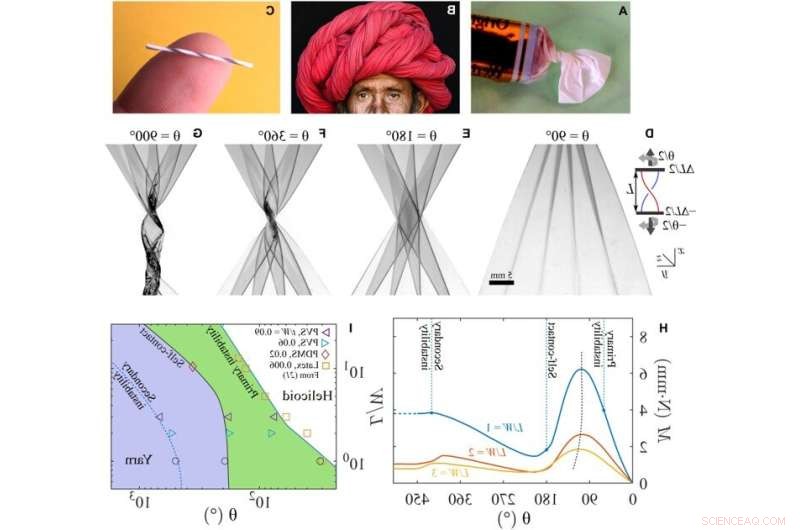
Experiment avslöjar en mycket ordnad omvandling till garn när ark som hålls under spänning vrids bortom början av primära instabiliteter. Exempel på tvinnade, vikta och rullade strukturer är följande:(A) inslagna godis, (B) multifunktionella Rajashtani Turban (foto:Lauren Cohen), och (C) rullat garn från ett polyetenark (se avsnitt S4). (D till G) Skuggbilder av ett transparent PDMS-ark vridet genom vinkeln θ som visas i insättningen (L/W =1; t/W =0,0028; ΔL/L =0,1; θp =60 ± 5°). Insättning:Schematiskt och labbkoordinatsystem. (D) Rynkor observerade strax ovanför början av primär instabilitet. (E) Dragspel vikt ark med självkontakt. (F) En kapslad helicoid med vikta lager som utvecklas när arket vrids ytterligare. (G) Sekundär knäckningsinstabilitet uppstår med ytterligare vridning, vilket resulterar i en garnliknande struktur. Skalstapeln är densamma i (D) till (G). (H) Det uppmätta vridmomentet visar en upprepad ökande och minskande sågtandsvariation med vridning. Variationens amplitud ökar när L/W minskar. (I) En karta som avgränsar regioner där den primära instabiliteten, självkontakten och den sekundära instabiliteten uppstår som en funktion av bildförhållande och vridning. Linjer är guider för ögat, förutom den primära instabiliteten för L/W> 3. Kredit:Science Advances (2022). DOI:10.1126/sciadv.abi8818
I en ny studie som nu publicerats som en rapport och även illustrerad som onlineförsättssidan för Science Advances , Julien Chopin, Arshad Kudrolli och ett forskarlag i fysik i USA och Brasilien visade hur tvinnade hyperelastiska ark bildade flerlagers självrullande garn. Genom att införliva dominant sträckning med vikningskinematik, mätte de vridmoment och energi som härrörde från geometriska olinjäriteter. De introducerade sedan en geometrisk modell för att förklara bildningen och strukturen hos sådana självrullade garner. Resultaten visade hur en enkel vridning av origami i det spänningsfallande ramverket ledde till förvandlingen av töjbara ark till självmonterade arkitekturer.
Formomvandling av ark
Traditionellt kan tvinnade ark bilda funktionella garner som förlitar sig på årtusenden av mänsklig praxis för att bilda catgut-bågsnören, kirurgiska suturer och tygmaterial; emellertid saknar praktiken fortfarande övergripande principer som vägleder inveckladheten i sådana arkitekturer. Rullade garn med kapslade strukturer kan användas för att utnyttja energi på batterier och för att bädda in amorfa material. Twistvikning kan förvandla platta ark till skiktade strukturer via fjärrstyrning av gränser. Vrid-vikning och rullning kan användas för att omkonfigurera och återanvända platta ark som sett med den multifunktionella Rajasthan-turbanen.
För att förstå formtransformation av ark och samspelet mellan topologi och stora formtransformationer använde Chopin et al tredimensionell röntgenskanning för att detaljera den spontana bildningen av tvinnade, flerskiktiga garner med ordnade interna arkitekturer. Det är dock fortfarande utmanande att modellera de stora formtransformationerna och konfigurationerna. Nyligen genomförda studier har inkorporerat elastiska plattmodeller inklusive Föppl–von Kármán (FvK) ekvationen för att lösa den initiala tillväxten ovanför början av primär instabilitet, men sådana metoder återstår för att förklara omvandlingen av ett platt ark till rullade garner. I detta arbete utvecklade Chopin et al ett nytt ramverk för att kombinera kinematiken hos strukturerade ark och använde origami för att förklara dessa observationer. Teamet visade hur de vikta arken visade regelbundna polygonala former som beskrivs av Schläfli-symboler och hur origami-kinematik fångade strukturens huvuddrag för att ge ett ramverk som fungerade som en guide för att utveckla hyperelastiska material med breda tillämpningar.
Online-omslag:Ett tunt ark av polydimetylsiloxan (PDMS) tvinnas till flerskiktsrullat garn. I årtusenden har människor vridit töjbara lakan för att bilda funktionella garn för att skapa klädesplagg, stränginstrument och upcycle-plast. Chopin och Kudrolli, utvecklar en elasto-geometrisk ram för att förstå de fysiska mekanismerna som är involverade i att vrida töjbara ark till självmonterade arkitekturer för avancerade tillverkningsstrategier. Kredit:Science Advances (2022). DOI:10.1126/sciadv.abi8818
Teamet visade exempel på polydimetylsiloxan (PDMS) ark med ökande twist. När den applicerade vridningen ökade ytterligare, noterade de bildandet av en kapslad spiralformad struktur i midjan, följt av sekundära instabiliteter och resulterande rekursiv vikning och ett rullat flerskiktsgarn. Varje större formomvandling fick ändringshastigheten för applicerat vridmoment att ändra tecken och bilda en sågtandsvariation med en vridning.
Chopin et al illustrerade spänningsvridningsramverket för att förstå de observerade huvudstadierna av transformation av ett plant ark till självrullande garn. De åstadkom detta genom att introducera en uppsättning modeller för att kombinera geometri, elasticitet och kinematik för att sedan fånga de observerade formtransformationerna. Forskarna fångade den lagrade elastiska energin och vridningsresponsen och följde detta arbete med 3D-röntgentomografi för att rekonstruera vridna polyvinylsiloxan (PVS) ark. Forskarna beräknade sedan böjningsenergidensiteten med hjälp av ark med olika Youngs moduler och karakteriserade överföringen med vridning.
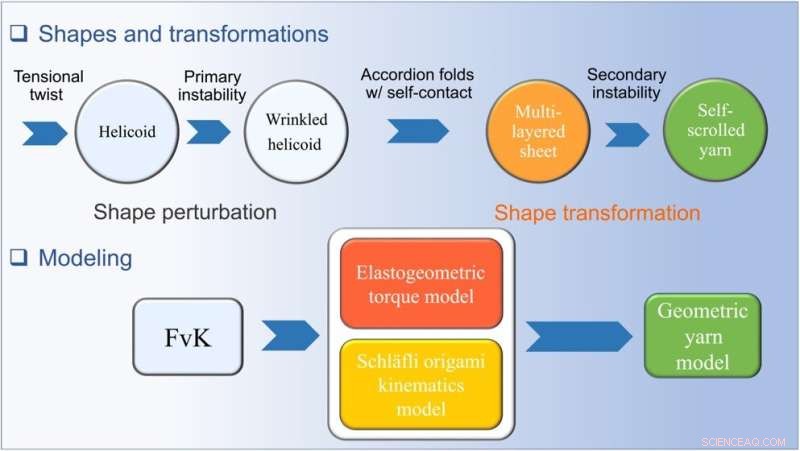
En översikt över observationstransformationerna med vridning och det spänningsvrid-vikbara ramverket. De observerade huvudtransformationerna som ett plant ark upplever spänningsvridning och rullning med applicerad vridning. Det elastogeometriska ramverket visas, inklusive den störande FvK-formalismen, den elastogeometriska vridmomentmodellen som innehåller geometriska olinjäriteter för att förklara spännings-töjningsrelationen med vridning, den kinematiska modellen för Schläfli-origami och den geometriska garnmodellen. Kredit:Science Advances (2022). DOI:10.1126/sciadv.abi8818
Elastogeometrisk vridmomentmodell, självvikbar och Schläfli-origami
Baserat på de experimentella observationerna utvecklade Chopin et al en elastogeometrisk modell för att beräkna den lagrade elastiska energin och vridningsresponsen hos arket. De åstadkom detta genom att hämta inspiration från spänningsfältteorin för att beskriva mycket skrynkliga plåtar, där böj- och tryckspänningar var försumbara jämfört med dragflätor. Liksom i spänningsfältteorin antog Chopin et al att energin under veckning till övervägande del gavs av sträckningslägen i längdriktningen, medan böjningslägena var subdominerande. Teamet jämförde det uppmätta vridmomentet som en funktion av vridning i förhållande till materialets hyperelastiska natur och kompletterade sin elastogeometriska analys med origamikonstruktion för att visa god överensstämmelse mellan origamiformen och det vridna arket. Forskarna identifierade sedan dessa origami med Schläfli-symboler, som de sedan döpte till Schläfli-origami. Genom att variera Schläfli-symbolerna fick Chopin et al triangel-, femhörnings-, halvkants- och icke-hörnformade kuvert. Arbetet belyste hur origami-kinematik underbyggde spänningsvridning.
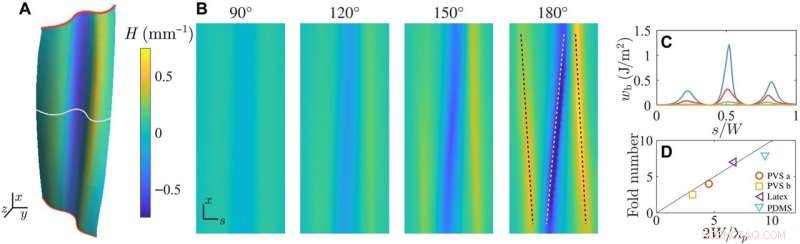
Dragspelsvikning genom krökningslokalisering. (A) Deformationen av ett polyvinylsiloxan (PVS)-ark vridet med θ =120° erhållen med röntgentomografi och återgiven med medelkrökning H som ges av färgfältet till höger (L/W =3; t/W =0,009; 6p =75° ± 5°). De centrala 80 % av arket bort från klämmorna visas. (B) Den rumsliga fördelningen H mappad till en rektangulär domän visar symmetribrott och lokalisering av arkets krökning med vridning. (C) Böjningsinnehåll wb visar lokaliseringen av energi med veck över tvärsnittet som indikeras av den heldragna vita linjen i (A). (D) Det uppmätta antalet veck n jämfört med förhållandet som ges av våglängden för den primära instabiliteten n =2W/λp. Bildförhållandena (t/W, L/W) är som följer:PVS a (0,009,2), PVS b (0,006,3), PDMS (0,003,1) och latex (0,003,2). De tre materialen är hyperelastiska med Youngs modul E =1,2 MPa (PVS), 6,2 MPa (PDMS) och 3,6 MPa (latex). Kredit:Science Advances (2022). DOI:10.1126/sciadv.abi8818
Garnbildning och den geometriska garnmodellen
För att modellera garntillväxt antog Chopin et al att arket kunde delas in i tre sektioner, för att inkludera en garnliknande längdstruktur och två solfjäderliknande strukturer. Denna förenkling gjorde det möjligt för dem att behålla den grundläggande rollen som den vridna plåtkanten i den elastogeometriska vridmomentmodellen. De studerade också utvecklingen av garnlängd genom att spiralformigt linda fläktkanterna runt en cylindrisk kärna med en specifik diameter för att slutligen bilda en tillväxtmodell i god överensstämmelse med experimentdata.
Partiell Schläfli-origami förklarar skiktade arkitekturer i halvvridning. (A) Geometriska former som erhålls genom att öka Schläfli-symbolerna och antalet fasetter. (B) Jämförelse av det experimentella radiogrammet och Schläfli fold origami. God korrespondens observeras i alla fyra fallen. (C) Vinkeln Ψi för det i:te vecket som en funktion av den beräknade vinkeln i α med hjälp av den geometriska modellen överensstämmer utmärkt. (D) Jämförelse av spetsvinkeln α som en funktion beräknad α med hjälp av olika ark och belastning. (E) Spetsvinkeln som funktion av triangelnummer är i huvudsak konstant. Kredit:Science Advances (2022). DOI:10.1126/sciadv.abi8818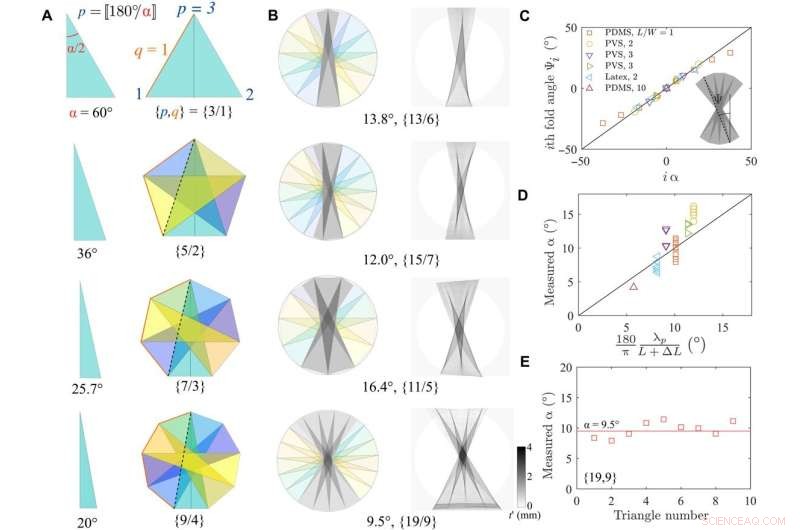
På detta sätt beskrev Julien Chopin, Arshad Kudrolli och kollegor den anmärkningsvärt ordnade förvandlingen av platta ark till rullade flerskiktsgarner. De åstadkom detta genom att introducera en serie förenklade elastogeometriska modeller för att bilda en vridvikbar ram. Teamet utforskade den platta flerskiktsstrukturen genom att introducera en Schläfli-origamimodell, där origamin, när den vrids av ett halvt varv, bildade regelbundna stjärnformade polygoner som kännetecknas av Schläfli-symboler. Chopin et al använde röntgentomografianalys för att förklara utvecklingen av arket och indikerade sammansättningen av ett mycket tvinnat garnområde i mitten och svagt tvinnade solfjäderliknande områden kopplade till de två klämmorna. Modellen som ingår i detta arbete baserades på förenklad kinematik för att tillhandahålla ett ramverk för att möjliggöra multifunktionella garn med ultratunna polymerer, kolnanorör och grafenark, lämpliga som material med tillämpningar inom medicin och flexibel elektronik. Forskarna använde PDMS (polydimetylsiloxan) och PVS (polyvinylsiloxan) polymerer på grund av deras hyperelasticitet under olika belastningsförhållanden. Den resulterande sträckvikningsstrategin kan skapa omplacerbara funktionella strukturer från enkla element för avancerad tillverkning med mjuka material. + Utforska vidare
© 2022 Science X Network