Geometri är fullspäckad med terminologi som exakt beskriver hur olika punkter, linjer, ytor och andra dimensionella element interagerar med varandra. Ibland är de löjligt komplicerade, som rhombicosidodecahedron, som vi tror har något att göra med antingen "Star Trek" maskhål eller polygoner. Eller vad sägs om den 12-sidiga dodekaedern?

Andra gånger är vi begåvade med enklare termer, som motsvarande vinklar .

Men innan vi förklarar vad de är, låt oss snabbt gå igenom några grundläggande begrepp.

Till att börja med, minns du definitionen av en vinkel? Det är vad du får när två strålar (linjer med en enda ändpunkt) förenas vid en punkt. Avståndet mellan de två strålarna är vinkeln .

Parallella linjer är två linjer på ett tvådimensionellt plan som aldrig korsar varandra, oavsett hur långa dessa linjer blir.

Sedan har vi tvärgående linjer . Det här är helt enkelt ett snyggt sätt att namnge en linje som korsar minst två andra linjer.

Nu går vi in ​​i magin. För när en tvärgående linje korsar två parallella linjer är vinklarna som blir resultatet av dessa skärningar väldigt speciella. Det vill säga att paren av vinklar på samma sida av transversalen – och i samma position för varje linje som transversalen korsar – har samma vinkel. Med andra ord, dessa vinklar är kongruenta (samma).

Om det inte är klart, kanske Merriam-Webster-definitionen hjälper. Det står att motsvarande vinklar är "vilket par av vinklar som helst som var och en är på samma sida av en av två linjer som skärs av en tvärgående och på samma sida av den tvärgående."

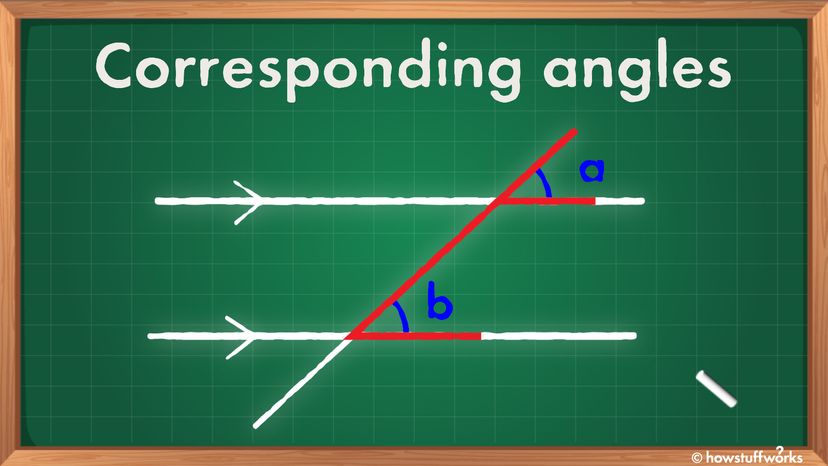
I huvudbilden ovan är motsvarande vinklar märkta "a" och "b." De har samma vinkel. Du kan alltid hitta motsvarande vinklar genom att leta efter F-formationen (antingen framåt eller bakåt), markerad i rött. Här är ett annat exempel på bilden nedan.

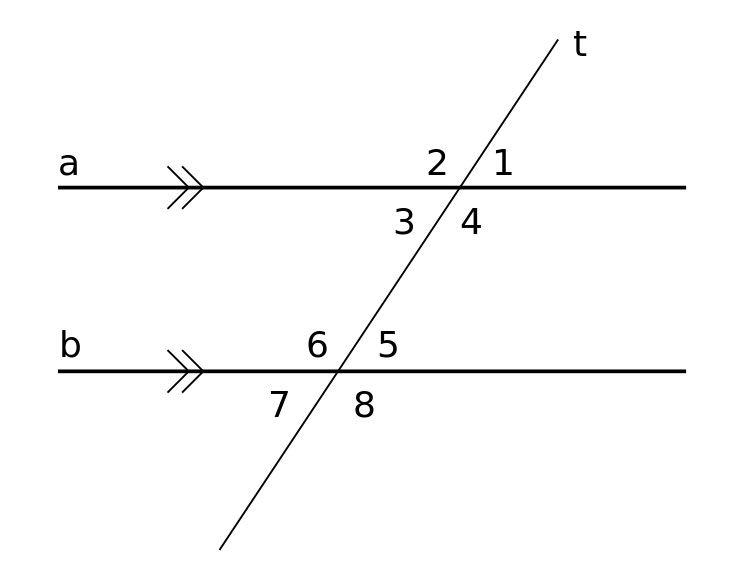
John Pauly är en matematiklärare på mellanstadiet som använder en mängd olika sätt att förklara motsvarande vinklar för sina elever. Han säger att många av hans elever kämpar för att identifiera dessa vinklar i ett diagram.

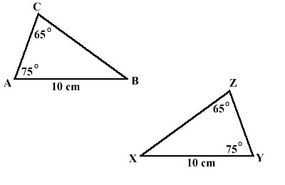
Han säger till exempel att ta två liknande trianglar, trianglar som har samma form men inte nödvändigtvis lika stora. dessa olika former kan omvandlas. De kan ha ändrats storlek, roterats eller reflekterats.

I vissa situationer kan du anta vissa saker om motsvarande vinklar.

Ta till exempel två figurer som är lika, vilket betyder att de har samma form men inte nödvändigtvis samma storlek. Om två figurer är lika, är deras motsvarande vinklar kongruenta (samma). Det är jättebra, säger Pauly, eftersom det gör att figurerna kan behålla sin form.

Han säger att du ska tänka på en bild du vill passa in i ett dokument. "Du vet att om du ändrar storlek på bilden måste du dra från ett visst hörn. Om du inte gör det kommer motsvarande vinklar inte att vara kongruenta, med andra ord kommer det att se knasigt ut och ur proportion. Detta fungerar också för omvänt. Om du försöker göra en skalenlig modell vet du att alla motsvarande vinklar måste vara samma (kongruenta) för att få exakt den kopia du letar efter."

Nu är det intressant

Som med alla matematikrelaterade begrepp vill elever ofta veta varför motsvarande vinklar är användbara. "Tja, om du vill vara säker på att du har två linjer som är parallella kan du använda det här lilla tricket", sa Pauly. "Varför inte rita en rät linje som skär båda linjerna och sedan mäta motsvarande vinklar." Om de är kongruenta vet du att du har mätt och klippt dina bitar ordentligt. Att känna till motsvarande vinklar är användbart när man bygger järnvägar, höghus och andra strukturer.