Forskare från University of Ottawa (uOttawa), i samarbete med Weizmann Institute of Science och Lancaster University, har observerat en dold kvantövergång som bara kan ses beroende på hur observatörer utför mätningar.
Studien "Topological Transitions of the generalized Pancharatnam-Berry phase" publicerades i Science Advances den 24 november 2023.
En väsentlig del av den vetenskapliga metoden förlitar sig på förmågan att mäta resultatet av ett experiment exakt och att jämföra dessa resultat med tidigare resultat. Forskare utvecklar mätinstrument, eller mätare, som gör det möjligt för dem att exakt kvantifiera storleken på fysikaliska egenskaper. Men "mätningsprocessen" väcker en kritisk och spännande fråga:förändrar processen att mäta en parameter systemet som mäts?
Inom fysiken tror man ofta att påverkan på systemet är försumbar. Ändå kan samma antagande inte göras i samband med kvantmekaniken, eftersom mätningen avsevärt kan påverka systemet under observation.
Forskargruppen, ledd av Yuval Gefen, professor vid fysikfakulteten vid Weizmann Institute of Science och Ebrahim Karimi, professor i fysik och Kanadas forskningsstol i strukturerade kvantvågor vid naturvetenskapliga fakulteten vid University of Ottawa, tog fram en sofistikerad protokoll för att observera denna mätningsdrivna topologiska övergång.
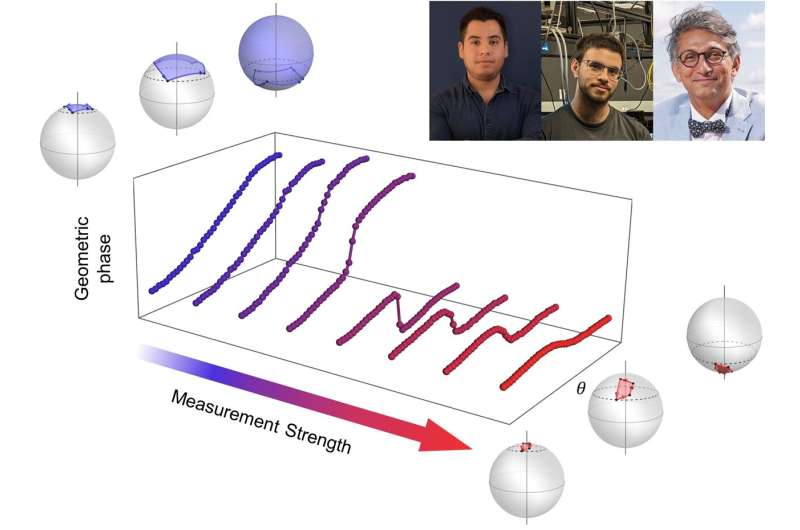
Detta protokoll innebar en cyklisk sekvens av mätningar med varierande styrkor - från stark till svag - på polarisationstillståndet för fotoner som emitteras från en laserkälla. Deras resultat avslöjar att även om den topologiska övergången förblir intakt trots förekomsten av ofullkomligheter i både systemet och processen, är den också känslig för dessa ofullkomligheter.
"Denna känslighet manifesterar sig i betydande förändringar i övergångens läge och form, vilket understryker den känsliga balansen mellan systemintegritet och yttre påverkan i sådana avancerade vetenskapliga undersökningar", säger Manuel F. Ferrer-Garcia, Ph.D. kandidat, som genomförde laboratorieexperimentet vid Nexus for Quantum Technologies Institute i uOttawa.
Inom kvantmekaniken är det allmänt accepterat att hela ett kvantsystems tillstånd är inkapslat i dess vågfunktion. För att lära sig om tillståndet interagerar systemet med en mätanordning, det vill säga mätare, som är avgörande för att kvantifiera storleken på en fysisk egenskap. Konventionellt använder kvantforskare en teknik som kallas projektiva mätningar i sitt laboratorium.
Dessa mätningar anses vara "starka" eftersom de framkallar "kollaps" av vågfunktionen, där den reduceras till ett specifikt tillstånd i linje med ett av mätanordningens tillstånd. Denna process ger inte bara information utan förändrar också systemets initiala kvanttillstånd. Det är dock möjligt att ta fram ett mätprotokoll som minimalt påverkar systemet, vilket leder till något obestämda avläsningar på vår mätare.
Genom upprepade interaktioner blir det möjligt att samla information om systemet, en process som kallas "svaga" mätningar. Från denna förståelse kan vi härleda potentialen för att designa mätprotokoll vars påverkan sträcker sig mellan dessa två ytterligheter - stark och svag. Detta koncept öppnar nya vägar för att utforska kvantsystem och deras interaktioner med mätanordningar, vilket markerar ett betydande framsteg inom kvantmätningstekniker.
En betydande men mindre uppenbar aspekt av kvantfenomen är deras djupa koppling till topologiska begrepp. Topologi är i huvudsak en gren av matematiken som fokuserar på studiet av egenskaper som är invarianta eller förändras diskontinuerligt under kontinuerliga deformationer. Ett exempel på dessa invarianter är antalet hål i slutna ytor – t.ex. kan en sfär kontinuerligt omvandlas till en munkform, men antalet hål kommer plötsligt att ändras från noll till ett när två olika ytpunkter kommer i kontakt med varandra .
Topologiska invarianter spelar en viktig roll inom många områden av modern fysik. I detta arbete observerade forskarna en topologisk övergång när mätstyrkan ändras från stark till svag. Denna övergång involverade beteendet hos ett annat matematiskt koncept:den geometriska eller Pancharatnam-Berry-fasen.
När ett kvanttillstånd genomgår en cyklisk utveckling, d.v.s. det går tillbaka till det initiala tillståndet efter en tidsperiod, kan det förvärva en "global" fas, som enbart beror på krökningen av det utrymme där utvecklingen sker. Denna fas kan observeras genom att interferera med det utvecklade tillståndet med det initiala.
Effekten av denna forskning går utöver omfattningen av fundamental fysik. Eftersom övergången visade sig vara känslig för vissa egenskaper hos kvantsystemet, har den potential att användas vid avkänningstillämpningar eller karakterisering av optiska element.
Mer information: Manuel F. Ferrer-Garcia et al, Topological transitions of the generalized Pancharatnam-Berry phase, Science Advances (2023). DOI:10.1126/sciadv.adg6810
Journalinformation: Vetenskapens framsteg
Tillhandahålls av University of Ottawa