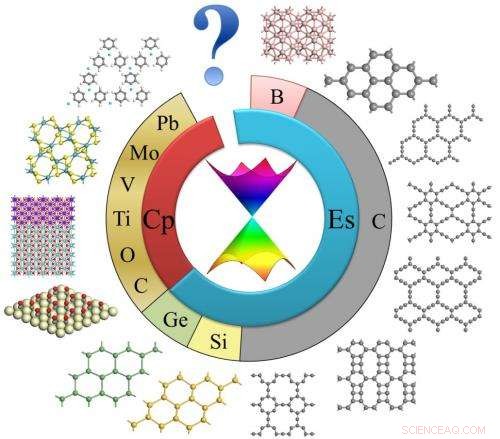
Schema för 2-D-material med Dirac-kottar. Upphovsman:© Science China Press
Grafen, ett tvådimensionellt (2D) bikakeark som består av kolatomer, har lockat intensiva intressen över hela världen på grund av sina enastående egenskaper och lovande framtidsutsikter inom både grundläggande och tillämpad vetenskap. Den stora utvecklingen av grafen är nära besläktad med den unika elektroniska strukturen, det är, Dirac kottar. Konen som representerar linjär energidispersion på Fermi -nivå ger grafen masslösa fermioner, som leder till olika quantum Hall -effekter, ultrahög transportörrörlighet, och många andra nya fenomen och egenskaper.
Dirac cone är speciell men kanske inte unik för grafen. Nyligen, allt fler 2D -material har förutspåtts ha Dirac -kottar, såsom silen och germanen (grafenliknande kisel och germanium, respektive), flera grafyner (sp-sp2 kolallotroper), och så vidare. Men dessa 2D Dirac -system är så sällsynta jämfört med de många 2D -materialen. En djup förståelse för alla kända 2D Dirac -system och en strategi för att söka efter nya behövs.
Ett nytt papper publicerat i National Science Review presenterade de senaste framstegen med teoretiska studier av olika 2D Dirac -material.
I det här pappret, strukturens och elektroniska egenskaper hos grafen, silen, tyska, grafyner, flera bor- och kolallotroper, övergångsmetalloxider, organiska och organometalliska kristaller, kvadrat MoS2, och konstgjorda gitter (elektrongaser och ultrakylda atomer) sammanfattades. Som författaren sa, "de flesta Dirac -material har rumslig inversionssymmetri", "Många av dem är tvåpartiga och består av endast ett element", och "hexagonal bikakestruktur är vanlig i atomiska Dirac -material". Eftersom "Dirac-cone-strukturen ger grafen masslösa fermioner, vilket leder till halvtal/fraktion/fraktal kvant Hall-effekter, ultrahög bärarrörlighet ", andra 2D Dirac -system förutsades ha liknande egenskaper, och vissa har till och med ny fysik bortom grafen.
Baserat på ovanstående diskussioner, författarna undersökte vidare hur Dirac -punkter rör sig och går samman i dessa system. De nämnde att stam kan flytta Dirac -punkten till en ny k (ömsesidig) plats. Men "när två Dirac -punkter med motsatta Berry -faser rör sig i k -utrymmet under någon störning och anländer till samma punkt, de smälter samman och deras Berry -faser förstör varandra ". Dessutom, von Neumann-Wigner-satsen tillämpades för att förklara bristen på 2D Dirac-system. Sedan drogs strikta krav på ett 2D -system för att uppnå Dirac -kottar, som är relaterad till symmetrin, parametrar, Fermi -nivå, och bandöverlappning.
Detta dokument noterade att "Dirac -kottar inte bara är den linjära energidispersionen kring diskreta punkter utan också singulariteter i spektrumet av Hamiltonians och är topologiskt skyddade." Författarna påpekade "Ser fram emot, vi tror att fler och fler 2D Dirac -material kommer att upptäckas, och en grundlig förståelse av de existerande förhållandena hos Dirac -kottar är till stor hjälp för att söka/designa nya system. "