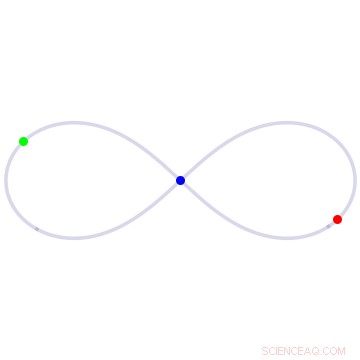
I figuren åtta lösningen på trekroppsproblemet, tre kroppar av lika stor massa jagar var och en runt en åtta-slinga. Kredit:University of California - Santa Cruz
Från dess ursprung för mer än 300 år sedan i Newtons arbete med planetbanor, trekroppsproblemet har utvecklats till ett rikt ämne som fortsätter att ge nya insikter för matematiker.
Richard Montgomery, en framstående professor i matematik vid UC Santa Cruz, kallar det en av de klassiska problematikerna i matematisk historia. I en artikel i augusti numret av Scientific American , han berättar om trekroppsproblemets historia och de framsteg som han och andra matematiker har gjort under de senaste två decennierna.
"Det har utmanat människor i århundraden, och det är delvis det som gör det intressant. Du lägger till arbetet av människor som Newton och Poincaré och Lagrange, sa Montgomery.
Det grundläggande problemet är att förutsäga rörelserna hos tre kroppar (som stjärnor eller planeter) som ömsesidigt attraheras av gravitationen, givet deras initiala positioner och hastigheter. Det visar sig att en generell lösning på problemet är i huvudsak omöjlig på grund av kaotisk dynamik, som Henri Poincaré upptäckte 1890.
"Det finns lösningar för speciella fall, men det finns ingen enkel formel för att ge dig en allmän lösning, " förklarade Montgomery.
Ur praktisk synvinkel att förutsäga planetariska banor och planera rymduppdrag, approximationer kan beräknas med en hög grad av noggrannhet med hjälp av datorer och en process som kallas numerisk integration. Det kan vara tillräckligt bra för NASA, men inte för matematiker, vars fortsatta utforskningar av problemet har lett till viktiga framsteg inom matematiken.
Fallande katter
Trekroppsproblemet binder samman tre olika grenar av matematiken:topologi, geometri, och dynamik. Montgomery sa att det var det som fick honom att intressera sig för det för mer än 20 år sedan. Han hade arbetat med frågor relaterade till matematik och fysik om hur en katt landar på fötterna, som har tillämpningar inom kontrollteori och satellitorientering.
"Jag fortsatte att förenkla problemet tills katten bestod av bara tre punktmassor, " sa Montgomery. Sedan hänvisade en kollega honom till en annan matematiker som hade arbetat med liknande idéer, och snart hade han bytt från fallande katter till himlamekanik. Att höra att de bästa människorna som arbetar med himlamekanik var i Paris, Montgomery tillbringade ett sabbatsår där och arbetade med Alain Chenciner vid Paris Diderot University på trekroppsproblemet.
Ett av deras första stora resultat, publicerades 2000, var en återupptäckt och bevis på en lösning i form av åttasiffror, där tre lika stora kroppar jagar varandra oändligt runt en åttaslinga. Även om Chris Moore från Santa Fe Institute först hittade denna lösning 1993, med hjälp av en numerisk approximationsmetod, dess återupptäckt av Montgomery och Chenciner hade en mycket större inverkan på fältet.
"Vi kunde ge ett rigoröst existensbevis för lösningen med siffran åtta, och sättet vi gjorde det på gjorde det möjligt för andra att generalisera lösningen och hitta en massa andra intressanta saker, " förklarade Montgomery.
Ett mer allmänt uttalande om trekroppsproblemet för valfritt antal kroppar större än två kallas N-kroppsproblemet. Montgomery sa när han först presenterade lösningen med tre kroppar åtta på en konferens, en medlem i publiken påpekade snabbt hur det skulle fungera för fyra kroppar. Snart, matematiker upptäckte en mångfald av nya banor för N-kroppsproblemet med lika massa. Dessa periodiska lösningar där alla massorna jagar varandra runt ett fast, stängd kurva utan kollisioner kallades "koreografier" av den spanske matematikern Carles Simó, som har upptäckt hundratals av dem.
"Det skapade en miniindustri, så att vi nu känner till ett stort antal av dessa koreografier, sa Montgomery.
Ny riktning
År senare, Simó hjälpte till att skicka Montgomerys forskning om trekroppsproblemet i en ny riktning genom att föreslå att han letade efter dynamiska mekanismer som ligger bakom de periodiska lösningarna. Detta ledde till ett produktivt samarbete de senaste åren med Rick Moeckel från University of Minnesota.
De nya matematiska idéerna som har dykt upp från Montgomerys arbete med trekroppsproblemet har inga praktiska tillämpningar, åtminstone inte ännu. Det är ofta så att abstrakta matematiska begrepp utvecklas långt innan någon finner en praktisk användning för dem.
Många människor har fängslats av det estetiska tilltalande av åttafigurslösningen och andra koreografier. Konceptet har till och med tagit sig in i science fiction genom den kinesiska författaren Liu Cixin, vars roman The Three-Body Problem vann Hugo-priset 2015.
Men Montgomery säger att han aldrig skulle ha tagit itu med problemet om han inte hade haft anställning.
"Det är ett så svårt problem, och du vet inte om du kommer att göra några framsteg, " sa han. "Men uthållighet lönar sig ibland. Så jag uppskattar anställningssystemet, och även att kunna ta sabbatsår för att arbeta med medarbetare. Det är något med att fysiskt träffa människor som är så viktigt för att arbeta tillsammans."
I hans Scientific American artikel, Montgomery ger inte bara en detaljerad beskrivning av trekroppsproblemet, men också en fascinerande berättelse om de internationella samarbeten och personliga relationer som gjorde det möjligt för honom att göra framsteg på denna övertygande matematiska gåta.