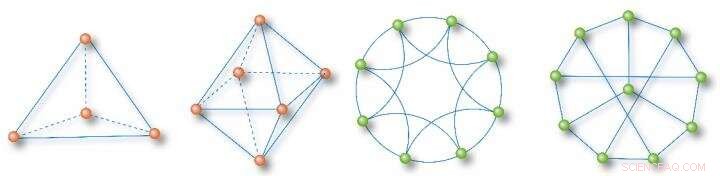
Helt homogena nätverksexempel:En tetraeder, ett minimalt nätverk med 2 håligheter, ett 8-noders närmaste grannnätverk, och ett 10-nodssynkroniseringsoptimalt nätverk Kredit:Science China Press
Sedan början av förra seklet har forskning om komplexa system har avancerat kaosområdena, fraktaler och nätverk. Ett nätverk består av noder och kanter, där noder representerar elementen i ett komplext system och kanter beskriver interaktionerna mellan dem. Sådana nod-edge-relationer kan representeras av en adjacensmatris, vars ordning är lika med antalet noder och varje radsumma motsvarar en nodgrad. Nodgradernas heterogenitet leder till framväxten av stjärnformade strukturer centrerade vid navnoder.
För att ta itu med heterogeniteten hos nodgrader, den skalfria nätverksmodellen spelade in, lockar bred uppmärksamhet. Hittills, allt eftersom internettekniken utvecklas och nätverksforskningen fortskrider, forskare har insett att den traditionella uppfattningen om stjärnbaserade heterogena nätverk är otillräcklig för att beskriva utvecklade komplexa nätverk och och nätverksvetenskapliga problem. Till exempel, det finns många nätgemenskaper på internet som är beroende av cykelbaserade sociala strukturer för gruppkommunikation och informationsspridning.
Nätverksfunktion och dynamiska egenskaper har fler och närmare förbindelser med högre ordnade nätverkstopologiska funktioner, homogena substrukturer och topologiska invarianter. Således, att flytta fokus från nodgrader till cykelnummer avslöjar många totalt homogena delnät i komplexa nätverk. Här, ett helt homogent nätverk definieras som ett nätverk med noder med samma grad, samma omkrets (antal kanter i nodens minsta cykel), och samma sökvägssumma (summan av kortaste vägar till en nod från alla andra noder). Några typiska exempel visas i figur 1 för illustration.
I slutet av 1800 -talet, Poincaré fann att gränser är viktiga för att skilja geometriska former som diskar, sfärer och tori. Han sönderdelade ett geometriskt objekt i grundläggande komponenter som kallas simplex (punkt, linje, triangel, tetraeder, etc.), och introducerade sedan begreppen homologigruppering, Betti-nummer och nod-edge-korrelationsmatris, och Euler-Poincaré-formeln, vilket visar att alternativ summering av simplex är lika med alternativ summering av Betti -tal.
Poincarés grundläggande idé är att dela upp en komplex geometrisk form för att förenkla proceduren för en lösning. Han kunde göra det eftersom det finns många totalt homogena delnät, såsom trianglar och tetraeder (kallas klickningar i grafteori eller simplex i topologi) i ett komplext nätverk. De är grundläggande strukturer för att stödja nätverksfunktioner - som skiljer sig från stjärnor, de är cykler. Med dessa grundläggande element, det är möjligt att beskriva ett nätverk med hjälp av en serie vektorutrymmen över det binära fältet.
Till exempel, vektorutrymmet har kanter som grund, med dimensionen lika med antalet kanter; vektorutrymmet har trianglar som grund, med dimensionen lika med antalet trianglar, och så vidare. Eftersom gränsen för en triangel består av kanter, de två intilliggande vektorutrymmena och kan korreleras via en gränsoperator, och dess gränsmatris kan användas för presentation och analys. Gränsmatrisen har ett rikare matematiskt innehåll och är mer användbart än adjacensmatrisen. Till exempel, med hjälp av gränsmatrisens rang kan man beräkna Betti -numret, en viktig invariant av nätverket, vilket är antalet linjärt oberoende hålrum av olika ordningar i nätverket, inrätta en homologigrupp. Figur 2 visar sambandet mellan vissa vektorutrymmen och deras motsvarande gränsoperatorer.
År 2002, Xiaofan Wang och Guanrong Chen publicerade det första kriteriet för nätverkssynkronisering. Det följdes av en serie verk inklusive introduktion av totalt homogena nätverk via optimering av Dinghua Shi, Guanrong Chen och Xiaoyong Yan 2013, avslöjar att det totalt homogena nätverket med en längre omkrets och en kortare vägsumma har en bättre synkronisering mellan nätverk av samma storlek. Dessutom, under 2006, Linyuan Lü och Tao Zhou använde H-operatören för att avslöja förhållandet mellan nodgrad, H-index och kärnvärde, fastställande av DHC -satsen. I undersökningen av cykelindex, ett viktigt arbete är den empiriska studien av Bassett et al. 2018 på hjärnans funktionella nätverk, där de påpekade vikten av klickar och hålrum för nätverksfunktion. Sist men inte minst, vi upptäckte nyligen det nära sambandet mellan Eulers karakteristiska nummer och nätverkssynkronisering.
Denna serie viktiga progressiva resultat visar betydelsen och betydelsen av tvärvetenskaplig forskning inom fysik, biologi och matematik. Med tanke på att denna nya riktning för nätverksstrukturanalys med algebraiska topologiska verktyg är lovande, forskarna valde att publicera sin nuvarande uppsats, "Helt homogena nätverk, " i National Science Review .
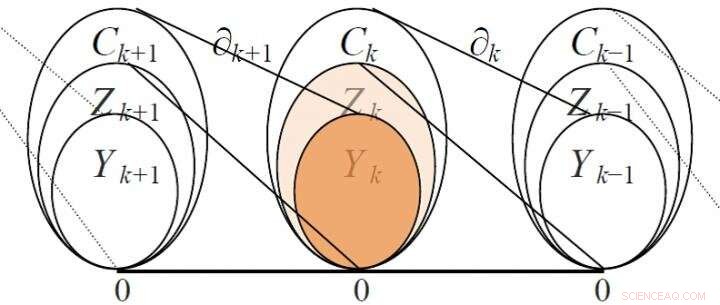
Förhållanden mellan vissa vektorrum och deras motsvarande gränsoperatorer (Zk är en cykelgrupp, Yk är en gränsgrupp) Kredit:Science China Press