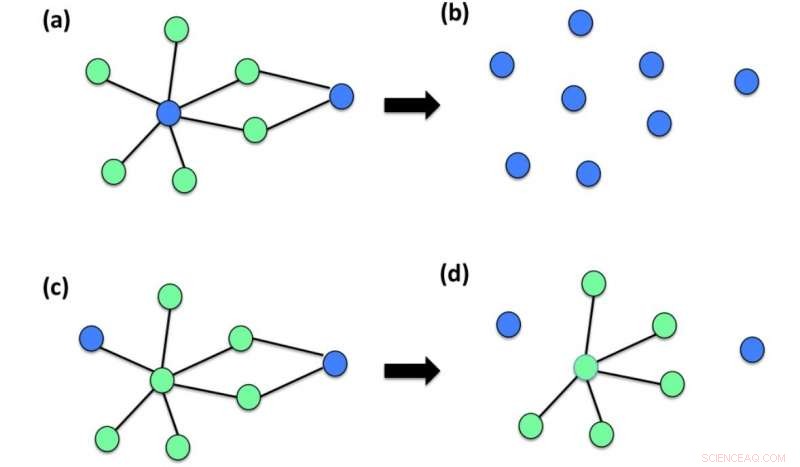
Olika insikter om den initiala skadan visar sig här vara mer eller mindre skadliga för ett nätverk. Panelen (a) visar en initial skada på ett anslutet nätverk som uteslutande påverkar två av N =8 -noder i nätverket (blå nod sindikat skadade noder gröna noder indikerar ej skadade noder). Panel (b) visar att denna initiala skada är mycket störande för nätverket och resulterar i en jättekomponent av storlek R =1. Panel (c) visar en annan initial skada -konfiguration av samma nätverk som endast påverkar två nätverksnoder. I detta fall visar panel (d) att effekten av skadan minskar och det mesta av nätet förblir anslutet vilket resulterar i en jättekomponent R =6. Kredit:Ginestra Bianconi
En teoretisk ram som förklarar risken för sällsynta händelser som orsakar stora störningar i komplexa nätverk, till exempel en strömavbrott i ett elnät, har föreslagits av en matematiker vid Queen Mary University of London.
Sällsynta händelser kan plötsligt demontera ett nätverk med mycket allvarligare konsekvenser än vanligt och att förstå deras sannolikhet är viktigt för att minska risken för att det händer.
Ett nätverk bildas av en uppsättning noder och länkarna mellan dem. Exempelvis är elnät nätverk vars noder är kraftstationer som är anslutna av det elektriska nätet. På samma sätt ett ekologiskt nätverk, som ramverket skulle kunna tillämpas på, bildas av arter som är anslutna genom ekologiska interaktioner som ett rovdjur-byte-förhållande.
Vanligtvis om några av noderna är skadade, nätverk som dessa är tillräckligt robusta för att förbli funktionella men i sällsynta fall kan specifika skador leda till att hela nätet demonteras och orsaka stora strömavbrott eller ekologiska regimskiften, som en ekologisk kollaps.
Matematiker använder ofta perkoleringsteori, en välutvecklad gren av tillämpad matematik som studerar nätverkets svar på skadan av en slumpmässig bråkdel av dess noder, för att belysa dessa fenomen. Dock, denna teori kan bara karakterisera ett nätverks genomsnittliga svar på slumpmässig skada. Därför kan förutsägelsen av det genomsnittliga beteendet inte användas för att uppskatta risken för ett nätverkskollaps till följd av en sällsynt händelse.
Denna studie fastställer en stor avvikelseteori om perkolering som kännetecknar svaret från ett nätverk på sällsynta händelser. Den föreslagna teoretiska ramen fångar korrekt effekten av sällsynta skador som kan observeras i verkliga nätverk. Intressant nog avslöjar arbetet att diskontinuerliga perkolationsövergångar - abrupta kollaps av ett nätverk - sker så snart sällsynta händelser beaktas.
Det teoretiska ramverket kan göra det möjligt att utveckla strategier för att upprätthålla nätverk genom att identifiera vilka noder som behöver bevaras för att förhindra en kollaps.
Ginestra Bianconi, författare till studien, sade:"Det finns ett brådskande behov av att utvärdera risken för kollaps som svar på sällsynta konfigurationer av initial skada. Detta resultat belyser nätverkens dolda bräcklighet och deras risk för en plötslig kollaps och kan vara särskilt användbar för att förstå mekanismer för att undvika katastrofal demontering av riktiga nätverk. "
Hon tillade:"Det är viktigt att uppskatta risken för en dramatisk kaskad av misslyckanden eftersom du vill minska risken. Vid utformningen av ett elnät som måste ge energi till ett helt land vill du undvika sällsynta händelser där du har stora strömavbrott, eller i utformningen av bevarande strategier för ett ekosystem som för närvarande är diversifierat och välmående vill du veta vad som är sannolikheten för en plötslig ekologisk kollaps och massutrotning. Därför är det nödvändigt att förstå denna risk för att dessa händelser inträffar. "
Den nuvarande stora avvikelsestudien om perkolering beaktar uteslutande nodperkolering på enstaka nätverk som de som nämns. Dock, Ginestra Bianconi föreslår att den skisserade metoden kan utvidgas till att studera mer detaljerade modeller för spridning av händelsefel.