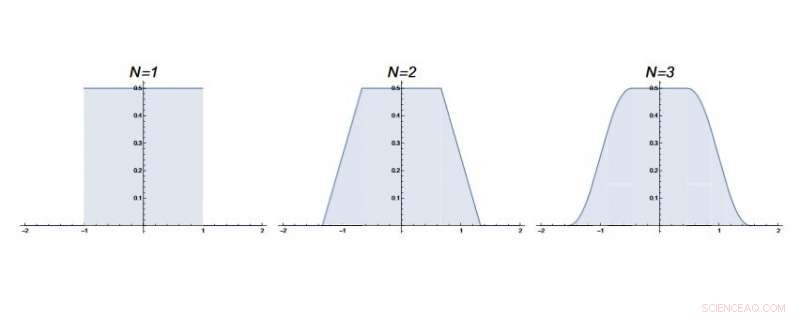
"Erosionen" av sannolikhetstätheten för slumpmässiga vandrare vid utgångspunkten vid det åttonde tidssteget (N ≥ 8, visas inte) ger en fysisk intuition om varför ett mönster som finns i vissa Borwein-integraler plötsligt bryter vid samma punkt. Kredit:Majumdar och Trizac. ©2019 American Physical Society
Mönster förekommer brett i naturen och matematiken, från Fibonacci-spiralerna av snäckskal till periodiciteten av kristaller. Men vissa matematiska problem kan ibland lura den mänskliga lösaren att se ett mönster, men då, ur det blå, mönstret försvinner plötsligt. Dessa illusiva mönster dyker upp inom många områden av matematiken, med ett exempel som kommer från vissa kalkylintegraler som har lurat intuitionen hos även de bästa matematikerna.
Nu i en ny studie, två fysiker har närmat sig dessa integraler med hjälp av fysikkonceptet slumpmässiga promenader. Att lösa dessa integraler vanligtvis kräver en hel del ansträngning och uppfinningsrikedom, fysikerna har visat att det nya tillvägagångssättet kan hitta lösningar intuitivt och ibland även utan behov av explicita beräkningar.
Fysikerna Satya N. Majumdar och Emmanuel Trizac vid universitetet i Paris-Sud, CNRS, i Frankrike, har publicerat en artikel om att använda slumpmässiga vandrare för att lösa integraler i ett färskt nummer av Fysiska granskningsbrev.
"Vi har visat att fysikinsikt gör att vi på ett beräkningsfritt sätt kan erhålla en mängd nyfikna integraler, och dessutom, för att erhålla tidigare okända identiteter (antingen integraler, eller likheter mellan diskreta summor och integraler), " berättade Trizac Phys.org . "Vårt arbete avslöjar att när matematisk intuition luras, fysisk intuition kan rädda dagen."
Mönster i Borwein-integraler
Integralerna i fråga (se figur) är "Borwein-integraler, " uppkallad efter David och Jonathan Borwein (far och son), som märkte ovanliga mönster i dem 2001. Borwein-integralerna involverar produkten av sinc (kardinalsinus) funktioner, som har utbredda tillämpningar, som inom optik, signalbehandling, och andra områden. Dessa två speciella integraler kan användas för att beräkna volymerna av hyperkuber.
Att lösa Borwein-integralerna innebär att ersätta variabeln med tal n . Varje nummer ger ett annat lösningsvärde, tillåter matematiker att observera mönster i den resulterande sekvensen av värden. Till exempel, för den första integralen (I n ), när du byter ut siffrorna n =1-7, du får svaret π varje gång. Men när du kommer till n =8, svaret är något mindre än π (ungefär π – 10 -10 ). Första gången matematiker beräknade detta värde på en dator, de trodde att det måste finnas en bugg i programvaran. Men svaret bekräftades, och de efterföljande villkoren (för n =9, 10, etc.) blir lite mindre.

Kredit:Majumdar och Trizac. ©2019 American Physical Society
Vissa mönster kvarstår ännu längre. För den andra integralen, J n , de första 56 termerna i sekvensen (erhålls genom att ersätta siffrorna 1 till 56 med n ) är alla π/2. Men 57:an th term är ungefär π/2—10 -110 , och de efterföljande villkoren fortsätter att minska. (Saker och ting kan bli ännu mer extrema:För en variant av Borwein-integralerna – som inte diskuteras här – gäller ett konstant värdemönster för en häpnadsväckande första 10 176 termer av sekvensen, varefter mönstret äntligen bryter.)
Matematiker kan förklara varför dessa mönster plötsligt bryter, åtminstone i matematiska termer. Lägg märke till att båda Borwein-integralerna ovan innehåller funktionen sinc(a n k), där en n =1/(2n—1). Om du ersätter siffrorna 1, 2, 3, … för n i detta uttryck, du får sekvens 1, 1/3, 1/5, 1/7, 1/9, ... . Borweins märkte att den första mandatperioden, 1, är inte bara större än alla andra termer som kommer efter, men det är ännu större än summan av de kommande termerna – den andra till den sjunde termen, för att vara exakt, som 1/3 + 1/5 + 1/7 + 1/9 + 1/11 + 1/13 =0,955… , vilket är mindre än 1. Men när man lägger till den åttonde termen, 1/15, till denna summa, svaret är 1,02... alltså strax över 1. Det visar sig att det inte är någon slump att den sjunde termen är den sista termen för vilken integralen evalueras till π, och den åttonde termen är punkten där mönstret bryter.
Borweinarna bevisade ett teorem (se figur) som uttrycker denna idé i mer allmänna termer. Satsen gäller för den andra integralen, J n , också. Redovisning för cosinusfunktionen i J n ändrar uttrycket ovan till 2/(2n—1), på grund av egenskapen cos(a)sinc(a) =sinc(2a), så att den första termen är 2 istället för 1. Som summan av den andra till 56 th termer i uttrycket är mindre än 2, men lägger till 57 th term trycker summan över 2, satsen gäller.
Slumpmässiga vandrare
Även om satsen hjälper till att förklara när Borwein-integralernas tillfälliga mönster bryter, det är fortfarande inte helt klart varför satsen håller i första hand.
I den nya tidningen, Majumdar och Trizac har erbjudit lite fysisk intuition i satsen genom att koppla den till några välförstådda begrepp inom sannolikhetsteori och statistisk mekanik. De märkte att integralen i satsen har nära kopplingar till den enhetliga sannolikhetsfördelningen, som används flitigt inom vetenskapen. Specifikt, Fouriertransformen av den enhetliga sannolikhetsfördelningen råkar bara vara sinc-funktionen, vilket ger Borwein-integralen för n =1. Denna förbindelse överbryggar Borwein-integralerna till den fysiska världen, så att genom att använda relevanta parametrar, händelser som följer en enhetlig fördelning kan användas för att modellera sekvensen av lösningar till Borwein-integralerna.
För att beskriva detta samband i ett mer fysiskt sammanhang, forskarna tittade på slumpmässiga vandrare. En random walker är ett abstrakt föremål som kan röra sig ett visst avstånd i vilken riktning som helst, där det exakta avståndet väljs slumpmässigt från ett kontinuerligt intervall av värden, och var och en av dessa värden är lika sannolikt att väljas (dvs. den följer en enhetlig fördelning). Random walkers kan noggrant modellera en mängd olika slumpmässiga fenomen, såsom börskurser, djurens vägar, och molekylernas vägar i en gas, som förekommer i en, två, eller tre dimensioner, respektive.
I den nya tidningen, the physicists show that the movements of infinitely many random walkers can be used to model the emergence and disappearance of the patterns in the Borwein integrals. To begin, the random walkers all start at the point zero on the one-dimensional number line. For the first step, each walker is allowed to move a random distance of up to 1 unit, either left or right. For the second step, each walker may move a random distance of up to 1/3, then a random distance of up to 1/5, then 1/7, 1/9, etc. That is, each successive allowable step distance corresponds to the next value of the expression 1/(2n—1).
The main question is, what is the fraction of random walkers at the starting point (the origin) after each time step? It turns out that the fraction (more precisely, the probability density) of walkers at the origin at each time step n corresponds to the solution to the Borwein integral using the same n värde.
As the physicists explain, for the first seven steps, the probability density that a walker ends up at the origin is always ½, which via the theorem above corresponds to an integral value of π. The key idea is that, up to this time, the density of walkers at the origin is the same as if the entire number line was uniformly populated with walkers. I verkligheten, as the maximum distance of each step is restricted, only part of the number line is accessible, d.v.s. the walkers' world is finite.
Dock, for the first seven steps, the walkers at the origin perceive that their world is infinite, since they do not possess any information about the existence of boundaries that would indicate that the world is finite. This is because none of those walkers that reached the outer boundary of their world (+1 or -1 after the first step) would have been able to make it back to the starting point in less than seven steps, even if taking the maximum size steps allowed and all in the direction toward the starting point. As these walkers had zero probability of showing up at the starting point before the eighth step, they could not affect the fraction of random walkers at the starting point. So for the first seven steps, the density of walkers at the origin is fixed at ½ (it is "protected").
But once those walkers that have reached +1 or -1 return to the origin, the situation changes. After the eighth step, it's possible that some of these walkers return to the starting point. Now these walkers act as "messengers" in the sense that their return to the starting point reveals the existence of a boundary, telling the other walkers at the origin that their world is finite, and therefore influencing the density of walkers at the origin.
Since these messenger walkers made it back to the starting point, it becomes clear that some other boundary-reaching walkers did not make it back, but instead may have kept continuing to move further away. Som ett resultat, the probability distribution becomes more spread out, causing the fraction of walkers at the origin to gradually erode from ½ (or π for the integral). It is this erosion that explains why the values of the first Borwein integral decrease ever so slightly for n ≥ 8. A similar argument holds for the second Borwein integral (see video).
By connecting the Borwein integrals to the probabilities of random walkers, the new results offer a completely different approach to solving these integrals than through direct calculation. The physicists showed that the same approach can be applied to many other integrals in addition to the two described here, including extensions to higher dimensions. The researchers expect that the approach has the potential to provide calculation-free solutions to many other integrals that are otherwise very difficult to solve.
"Random walk problems and their infinite ramifications form one of the cornerstones of modern physics with a wide range of applications in physics, chemistry, biologi, teknik, etc., " Trizac said. "Since our derivation of intriguing integrals involves basic concepts from random walk theory, we expect that new identities and integrals, with real-world applications, may be derived using our key idea in the near future."
© 2019 Science X Network