Om du någonsin har försökt lösa upp ett par hörsnäckor, du kommer att förstå hur öglor och sladdar kan vridas upp. DNA kan trassla in sig på samma sätt, och i vissa fall, måste skäras och återanslutas för att lösa knutarna. Nu ett team av matematiker, Biologer och datavetare har reda ut hur E. coli-bakterier kan ta bort trassligt DNA genom en lokal återkopplingsprocess. Matematiken bakom forskningen, nyligen publicerad i Vetenskapliga rapporter , kan få konsekvenser långt utöver biologi.

E. coli-bakterier kan orsaka tarmsjukdomar, men de är också laboratoriearbetshästar. E. colis genom är en enkel cirkel av dubbelsträngat DNA. Innan en E. coli-cell delar sig, den cirkeln är kopierad. Om du öppnar den dubbla helixen för att kopiera den kastar vridningspåfrestningar på andra ställen ner i molekylen - precis som att linda upp en sladd på ett ställe kommer att få den att rullas över någon annanstans. Processen resulterar i två tvinnade slingor av DNA som passerar genom varandra som ett "magiska ringar"-trick.

För att skilja ringarna, E. coli använder ett enzym som kallas topoisomeras IV, som exakt skär ett DNA-segment, låter öglorna passera genom brytningen och förseglar sedan brytningen igen. Eftersom topoisomeras IV är så viktigt för bakterier, det är ett frestande mål för antibiotika som ciprofloxacin. Men när topoisomeras IV är frånvarande, ett annat enzymkomplex kan gå in för att utföra denna bortkoppling, även om det är mindre effektivt. Detta komplex introducerar två avbrott och avlänkar genom att återansluta de fyra lösa ändarna.

"Det finns andra sätt att koppla bort ringarna, men hur gör de det?" sa Mariel Vazquez, professor i matematik och i mikrobiologi och molekylär genetik vid University of California, Davis.

En väg, Vazquez sa, är att återkopplingsenzymer tar bort en länk i taget tills de når noll. Den lösningen gynnades av biologerna.

Men matematiker ser på problemet lite annorlunda. De förstår DNA:t som en flexibel kurva i tredimensionellt rum. Vissa punkter på kurvan kan brytas och återanslutas. Till en matematiker, det finns många potentiella vägar för återanslutningsprocesser att fungera – inklusive några där antalet länkar faktiskt går upp innan de går ner igen.

"Alla dessa är desamma för en matematiker, men inte till en biolog, " sa Vazquez. För att bestämma den mest troliga vägen och lösa problemet, de vände sig till beräkningsmodellering.

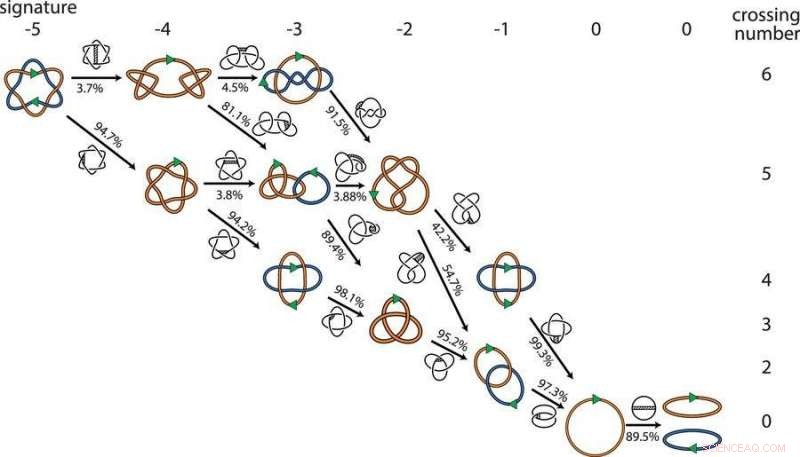
Vazquez och kollegor utvecklade datorprogramvara med DNA representerat som flexibla kedjor för att modellera de möjliga platserna där återkopplingsenzymer kunde klippa och återansluta kedjorna. Övergripande, de modellerade miljontals konfigurationer som representerade 881 olika topologier, eller matematiska former, och identifierade hundratals minimala vägar för att få två DNA-cirklar länkade på upp till nio platser ner till två separata cirklar.

Datormodellen bekräftade biologernas aning:Att ångra en länk i taget är den föredragna vägen för att separera DNA-cirklarna.

Resultaten kan ha implikationer långt utöver DNA-biologi, sa Vazquez. Det finns andra exempel i naturen på föremål som kolliderar, bryta och återansluta – som dynamiken i länkade vätskevirvlar, eller mönstren som bildas av rökringar, till exempel. När solflammor kastas ut från solen, kraftfulla magnetfältslinjer korsar och återansluter.

"Matematiken är inte DNA-specifik, och beräkningen kan anpassas, sa Vazquez.