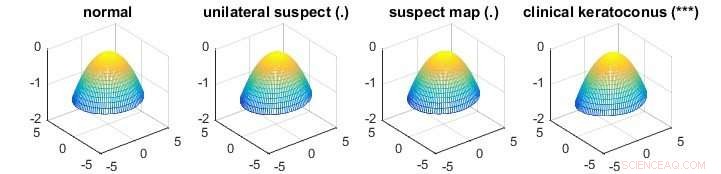
Figuren visar en tillämpning av den nya metoden för att identifiera skillnaden mellan medelhornhinneytor med varierande grad av keratokonussjukdomen som gör att hornhinnor missformas. Symboler inom parentes efter grupptitlarna indikerar den statistiska signifikansen av skillnaden mellan den associerade gruppen och den normala gruppen, där "***" betyder en mycket signifikant skillnad och "." tyder på en icke-signifikant skillnad. Hornhinnedataset är ett exempel på högdimensionell data. Den normala gruppen har 43 hornhinneytor medan den ensidiga misstänker, misstänkt karta, och kliniska keratokonusgrupper har 14, 21 respektive 72 hornhinneytor. Varje hornhinneyta har 6, 912 mätningar. De traditionella MANOVA-testerna är inte lämpliga för detta problem. Kredit:National University of Singapore
MANOVA (multivariatanalys av varians) är en vanlig statistisk metod inom dataanalys för att avgöra om det finns någon skillnad i medelvärden för olika grupper av data. Dock, det klassiska tillvägagångssättet är inte lämpligt för att analysera högdimensionella data. Högdimensionella data gör ofta de traditionella MANOVA-metoderna ogiltiga eftersom i en traditionell MANOVA, dimensionen antas vara fast och måste vara mycket mindre än antalet observationer. I en högdimensionell MANOVA-miljö, detta är inte längre sant. Prof ZHANG Jin-Ting från Institutionen för statistik och tillämpad sannolikhet, NUS och hans Ph.D. studenter har utvecklat en ny högdimensionell MANOVA-metod som kan användas för att effektivt jämföra medel för flera datagrupper som involverar högdimensionell data.
Den nya metoden lättar på många matematiska villkor och restriktioner som införts i litteraturen. En av dem är homoskedasticitetsantagandet. Detta antagande är ett matematiskt tillstånd som kräver att data från olika grupper har samma variationsmönster. Deras nya metod löser också de beräkningsproblem som är involverade i den praktiska implementeringen av MANOVA för högdimensionell data. Den gör detta genom att använda beräkningseffektiva matrisberäkningar på hög nivå.
Även om den är allmänt användbar och fungerar bra för många datauppsättningar i verkligheten, den föreslagna metoden kan vara mindre effektiv i vissa situationer eftersom variations- och korrelationsinformationen för variabler inte används fullt ut. Vid analys av hornhinneytor (se figur nedan), den associerade kovariansmatrisen som innehåller variations- och korrelationsinformationen från data beräknas. Om antalet hornhinneytor är större än antalet mätningar av en hornhinneyta, den beräknade kovariansmatrisen är inverterbar, vilket innebär att teststatistiken kan erhållas med det traditionella MANOVA-testet. I en högdimensionell miljö, detta är inte möjligt eftersom antalet hornhinneytor (150 =43+14+21+72 prover) är mycket mindre än antalet mätningar (6, 912 dimensioner). Dock, variations- och korrelationsinformationen används fortfarande delvis för att uppskatta parametrarna för teststatistiken. Prof Zhang och hans forskargrupp studerar detta för att utveckla bättre statistiska metoder som kan hantera sådana situationer.