
Jordens bergskedjor delar samma universella egenskaper. De blir synliga när den topografiska kartan (här:de liguriska alperna) förvandlas till en åskarta. (Källa:IFJ PAN) Kredit:Källa:IFJ PAN
Berg har karaktär. Den kontinuerliga milda, vågiga kullar och breda dalar i Karpaterna, Appalacherna eller de lägre delarna av Alperna står i stark kontrast till de skyhöga topparna, ojämna åsar och djupa raviner i de höga Tatrabergen och Pyrenéerna, vilka är, i tur och ordning, annorlunda än det otillgängliga, snötäckta Himalaya- eller Andinska jättar, längs vars sluttningar strömmar långa tungor av glaciärer i stället för vatten. Under denna stora mångfald, dock, ligger en förvånansvärt liknande struktur.
Med hjälp av grafer och fraktaler, forskare från Institutet för kärnfysik vid den polska vetenskapsakademin (IFJ PAN) i Krakow tittade på strukturen hos massiven på vår planet. Så olika områden som Alperna, Pyrenéerna, de skandinaviska bergen, de Baetiska bergen, Himalaya, Anderna, Appalacherna, Atlasbergen och södra Alperna gick alla under det statistiska förstoringsglaset. Analysen, presenteras i Journal of Complex Networks , resulterade i en oväntad observation. Det visar sig att det finns en universell likhet i strukturen hos jordens massiv. Det kan ses i bergskedjor på alla kontinenter, oavsett storleken på topparna, deras ålder, eller till och med om de är av tektoniskt eller vulkaniskt ursprung.
"Det verkar som att det enda som de olika bergskedjorna har gemensamt är att när man tittar på dem, du måste verkligen böja huvudet bakåt. Den verkliga likheten blir först synlig när vi förvandlar en enkel topografisk karta över bergen till en åskarta, dvs en som visar axlarna för alla åsar, " säger Dr Jaroslaw Kwapien (IFJ PAN), och tillägger sedan:"Åsens axel är en linje som löper längs toppen av bergsryggen på ett sådant sätt att terrängen på båda dess sidor faller nedåt. Den är alltså motsatsen till en dalaxel."
Bergsryggar är inte diskreta skapelser. De smälter samman till en stor, grenad struktur, som liknar ett träd:från huvudåsen ("stammen") finns längre eller kortare sidoåsar av första ordningen ("grenar"), från dem uppstår sidoryggar av andra ordningen, och från dessa efterföljande om och om igen. Det hela har en tydligt hierarkisk struktur och antalet grader av komplexitet beror på storleken på området täckt av berg och kan nå upp till flera dussin. Strukturer av denna typ presenteras i form av olika grafer. Till exempel, varje ås i ett givet massiv kan behandlas som en nod. Två noder är sammankopplade med linjer (grafens kanter) när motsvarande åsar också är sammankopplade. I den här typen av graf, vissa noder är anslutna till många noder, medan andra bara är anslutna till ett fåtal.
Grafer konstruerade för olika massiv har olika strukturer (topologi). Ett sätt att studera dessa är nodgradsfördelningen, innehållande information om antalet noder av en given grad. I typiska distributioner, stora värden visas vid noder av låg grad, eftersom de är de mest talrika. Det finns vanligtvis inte många noder av hög grad—hubbar. När det gäller berg, huvudnavet, vanligtvis motsvarar den längsta åsen av den studerade bergskedjan, har en grad på flera tusen. Andra ordningens nav, dvs sidoåsar på huvudåsen, har grader på flera hundra. De mest talrika är noder med graden ett. Det kan till och med finnas flera hundra tusen av dessa.
"Nodgradsfördelningen av åsarna visar sig vara av kraftlagskaraktär. Det betyder att antalet noder av en viss grad och, till exempel, antalet noder med en grad som är hälften så mycket står i en konstant relation, oavsett vald examen. Varje fragment av fördelningen ökad med en viss konstant faktor ser ut som en helhet, vilket innebär att ingen skala urskiljs, " säger Dr Kwapien.
Maktlagsfördelningar finns i grafer som representerar system som förekommer i naturen (t.ex. när man studerar kopplingarna mellan proteiner och enzymer i en levande cell), såväl som i våra egna aktiviteter (såsom citeringar av vetenskapliga artiklar, samarbete mellan skådespelare i filmer, omgivningen av ord i texter, länkar mellan webbplatser). De beskriver ofta sig själva, fraktala strukturer. Ett av modellexemplen på naturliga fraktaler är berg. Deras datormodeller genereras till och med av algoritmer som använder fraktalgeometri, så maktlagstopologin för åsgrafer borde inte förvåna någon. Dock, värdet på effektexponenten visade sig vara en överraskning.
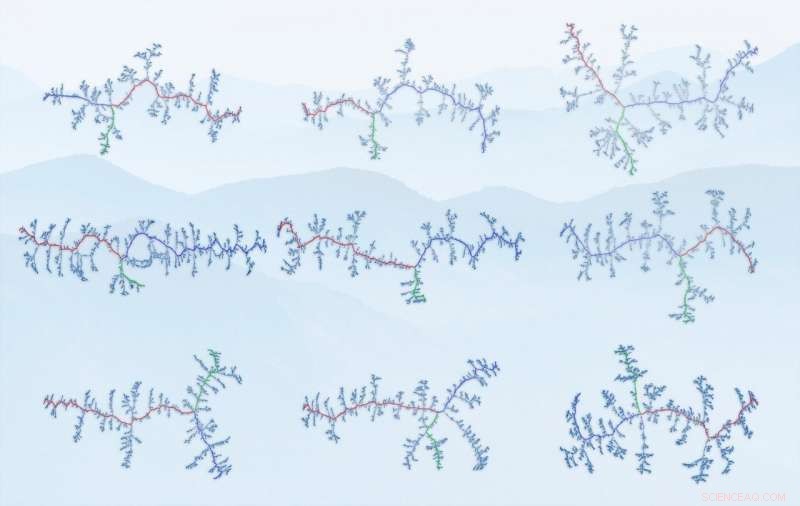
Åsdiagram över de studerade bergskedjorna. Noderna här är skärningspunkterna mellan åsar, kanterna - själva åsarna. Från övre vänster:Alperna, Baetic Mountains, Pyreneerna, Skandinaviska bergen, Himalaya (del), södra alperna, Appalacherna, Anderna (del), Atlasbergen. (Källa:IFJ PAN) Kredit:Källa:IFJ PAN
"Oavsett vilken typ av berg, exponenten för maktlagsfördelningen antog värden över ett mycket snävt område runt talet 5/3. Om vi tar hänsyn till noggrannheten i vår metodik, detta smala värdeintervall kan till och med betyda att exponenterna i varje undersökt fall var desamma, " konstaterar Dr Kwapien.
Den observerade homogeniteten härrör från det faktum att i alla delar av vår planet är de huvudsakliga mekanismerna som ansvarar för bergsskulptur i princip desamma. Tektoniska eller vulkaniska rörelser är nödvändiga för att höja terrängen, men den viktigaste skulpturfaktorn är vatten och glacial erosion. Vatten och is leder till sprickbildning och krossning av stenar och överför det fragmenterade materialet till låglandet. Detta resulterar i raviner, kanjoner och bergsdalar, och därför även åsar. Eftersom vattendragen som bildar avloppssystemet för ett givet område är av dendritisk struktur till sin natur (utanför ökenområden, självklart), en liknande struktur förekommer även i fallet med åssystemen. Men varför är de inbördes förhållandena mellan antalet åsar med olika antal grenar så lika för olika typer av berg?
"Situationen blir tydligare när vi beaktar gravitation utöver vatten, " förklarar Dr. Kwapien. "När stenmaterial krossas, den blir föremål för dynamiken hos lösa kroppar oavsett dess kemiska sammansättning. Lösa kroppar i sluttningar kan bara ligga kvar där om lutningsvinklarna inte är för stora. Backarna får inte vara för branta. Det är därför djupet av dalar i naturen begränsas av deras egen bredd. Smala flodkanjoner med nästan vertikala väggar finns bara i ett tidigt skede av skulpturbildningen. De är sällsynta i mogna bergsformationer eftersom deras väggar redan har lutat."
Förekomsten av flodsystem som dränerar vatten från ett givet område, erosion som krossar stenar och hugger dalar, liksom gravitationsskred av stenmassorna gör att åsarna inte kan vara godtyckligt nära eller långt från varandra. Det finns ett optimalt arrangemang, oberoende av bergskedjans egenskaper och ger bergen några universella egenskaper.
Ovanstående observationer kompletteras av en annan observation gjord av IFJ PAN-fysikerna, angående dimensionerna av fraktala åsstrukturer. Den fraktala dimensionen beskriver hur grov strukturen på objektet är. Linjen för en enda ås har dimensionen 1. Om linjerna (åsarna) var placerade extremt tätt, deras fraktala dimension skulle motsvara ytans dimension, och därför skulle vara lika med 2. Forskarna visade att om åsstrukturerna presenteras som grafer vars noder är skärningspunkterna mellan åsarna (det är i dessa skärningspunkter som toppar är vanligast), och kanterna på graferna är åsarna som förbinder topparna, då skulle fraktaldimensionerna för sådana grafer vara med en bra approximation lika med antalet... 5/3.
"I vissa grafer ser vi hierarkin av bergsstrukturer, hos andra deras fraktalitet. I båda fallen, för alla typer av berg möter vi samma värden på lämpliga siffror. Denna universalism ger stof till eftertanke, " konstaterar prof. Stanislaw Drozdz (IFJ PAN, Krakow tekniska universitet).
Om olika bergskedjor är så lika när det gäller storlek, var finns källorna till bergsmångfald? Kommer det att vara möjligt att studera dem med hjälp av grafteori och fraktalgeometri? Kommer det att vara möjligt att skapa en modell där en utvecklande graf kommer att imitera de successiva stadierna av bildandet av en bergsskulptur? Till sist, kommer det att vara möjligt att tillämpa omvandlingen av åskartor till grafer i praktiken, till exempel inom kartografi? Dessa frågor – och många andra – kommer bara att besvaras av framtida forskning.