En matematiker vid RUDN-universitetet har för första gången bevisat teoremet om existens och unika lösningar av Zakharov-Kuznetsov-ekvationen i en remsa. Sådana satser är mycket sällsynta för partiella differentialekvationer. De nya resultaten kan tillämpas inom områden som astrofysik, till exempel, i att beskriva utbredningen av plana vågor i plasma. Artikeln är publicerad i tidskriften Icke-linjär analys:Verkliga tillämpningar .

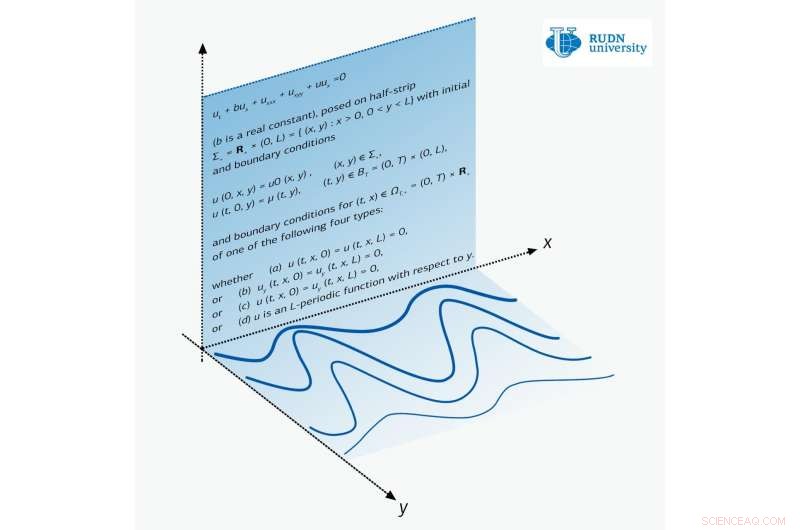
Zakharov-Kuznetsov-ekvationen är en enfunktionsekvation av två variabler x och y. För fysik, x är riktningen för vågens utbredning, och deformationen av mediet sker längs den vinkelräta riktningen y. Till exempel, i svängningen av en gitarrsträng, vågen ser ut att rinna nerför strängen, medan svängningarna sker vinkelrätt i förhållande till vågens gång.

Det finns ett stort antal resultat som beskriver lösningar av Zakharov-Kuznetsov-ekvationerna i fallet när det inte finns några begränsningar för y. Men frågan om vågutbredning i remsan - när y är begränsad - studerades inte omfattande förrän nyligen.

RUDN-universitetets matematiker behandlade Zakharov-Kuznetsov-ekvationen i remsan. De undersökte tre huvudfall - när det inte finns några svängningar på remsans gräns, när det inte finns någon ström på samma gräns, och när randvillkoren är periodiska till sin struktur. Det senare fallet motsvarar utbredningen av vågor i ett medium vars struktur är periodisk i x.

I alla dessa fall, matematiker lyckades bevisa existensens teorem och deras lösningars unika egenskaper. För system med partiella differentialekvationer, som inkluderar Zakharov-Kuznetsov-ekvationen, sådana ekvationer är mycket sällsynta.

Dessa resultat är de första för lösningar av ekvationen med initiala förhållanden i remsan. Platta plasmaflöden med randvillkor, som var bland de fenomen som forskare vid RUDN-universitetet betraktade, kan förekomma inom fysik och astrofysik.

Zakharov-Kuznetsov-ekvationerna tillhör en bredare kategori av ekvationer som kallas Korteweg-de Vries-ekvationerna. I studien av denna kategori av ekvationer, det är nu möjligt att beskriva solitoner – vågor vars form inte förändras under rörelse. Fysiker betraktar solitoner som ett verktyg för moderna optiska dataöverföringssystem. Studiet av solitoner, som kan uppstå i Zakharov-Kuznetsovs ekvationer, är ett av alternativen för att utveckla det arbete som utförs av RUDN-universitetets matematiker.