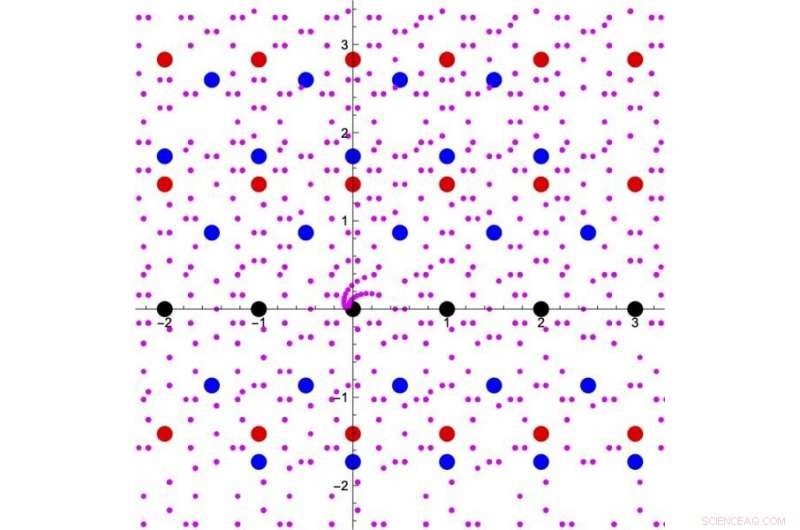
Figur 1. Utvidgning av begreppet integral "tal". Svarta punkter är de vanliga heltal som visas i ett komplext plan. Addition eller multiplikation av valfritt par av svarta punkter slutar med en annan svart punkt. Alla röda punkter och blå punkter i denna figur är lösningar på några andragradsekvationer med heltalskoefficienter. De lila punkterna är lösningar på några kvartsekvationer med heltalskoefficienter. Så, vi kan tänka på dessa punkter också som en del av "siffror". Additions- och multiplikationsoperationer mellan svarta eller röda punkter förblir inom "talen" som visas i svarta eller röda punkter, och liknande, dessa operationer av svart-röd-blå-eller-lila punkter förblir inom "siffrorna" i svart-röd-blå-eller-lila punkter. På det här sättet, det är möjligt att utöka uppsättningen av integral "nummer" gradvis. Kredit:Kavli IPMU
Ett samarbete mellan en matematiker och en fysiker har visat att de modulära formerna förknippade med elliptiska kurvor med komplexa multiplikationer uttrycks i termer av observerbara i supersträngteorin.
Begreppet tal kan utökas från heltal och rationella tal till att omfatta alla reella tal och komplexa tal, allt på en gång. Men det är också möjligt att utöka konceptet gradvis, genom att addera rötterna till polynom med rationella talkoefficienter (som kvadratroten ur 2 och kvadratroten ur 3) lite i taget (Figur 1). Denna speciella klass av komplexa tal kallas "tal". De exakta detaljerna om hur begreppet siffror kan utvidgas har ansetts vara ett av de viktiga teman inom talteorin.
I flera decennier, forskare har försökt ta itu med och förstå detta problem. Man skulle kunna specificera ett geometriskt objekt genom ekvationer med "siffrorna" först, och överväg sedan uppsättningen punkter i det geometriska objektet vars värden är "talen". När begreppet siffror gradvis utvidgas, och uppsättningen "siffror" utökades, fler och fler punkter i det geometriska objektet kommer att räknas (Figur 2). Tanken är att hur antalet punkter i det geometriska objektet ökar kommer att belysa hur uppsättningen "tal" expanderar. Vidare, denna information om tillväxthastigheten för antalet punkter i det geometriska objektet packas i en funktion som kallas den inversa Mellin-transformen av L-funktionen, som är en funktion som innehåller informationen om hur snabbt antalet punkter i ett geometriskt objekt växer när begreppet siffror utökas. Denna funktion har förväntats vara en modulär form, en funktion som förblir invariant under vissa operationer. Denna gissning är känd som Langlands gissning.
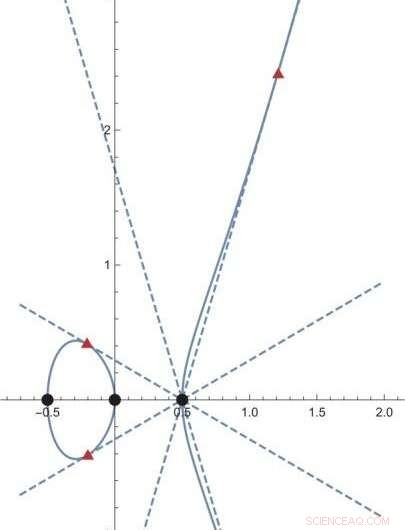
Figur 2. Ett geometriskt objekt givet av y^2 =4 x^3 - x visas med en tunn blå kurva. I detta objekt, de tre svarta punkterna har sina värden i de vanliga heltal. Å andra sidan, de tre punkterna i röda trianglar har sina värden i en mer utökad uppsättning "tal" (x-koordinaterna är av formen (p+q sqrt{2}) med rationella tal p och q; y-koordinaterna är mer komplicerade) . När begreppet "siffror" utökas, antalet poäng med sina värden i "siffrorna" ökar, även för ett givet geometriskt objekt. Kredit:Kavli IPMU
Kavli Institute for the Physics and Mathematics of the Universe (Kavli IPMU) Docent och partikelteoretiker Taizan Watari och aritmetisk geometriforskare vid Middle East Technical University Northern Cyprus Campus och Kavli IPMU Visiting Scientist Satoshi Kondo vågade fråga varför sådana funktioner är oföränderliga under vissa operationer.
I strängteorin, det är känt att en klass av observerbara (a) är invarianta under operationerna (x) som redan har hänvisats till. Invariansen under operationerna är en oumbärlig egenskap i den teoretiska konstruktionen av supersträngteorin. Så, forskarna visade att de omvända Mellin-transformerna av L-funktionerna för geometriobjekt (b) uttrycks i termer av ovanstående klass av observerbara objekt (a) i supersträngteorin med dessa geometriska objekt satta som målutrymmen. Som ett resultat, det följer att funktionerna som innehåller informationen om hur begreppet siffror utvidgas, den omvända Mellin transformerar, (b) bör vara invariant under vissa operationer, som bör vara modulära former, (x) av skäl ur supersträngteorin.
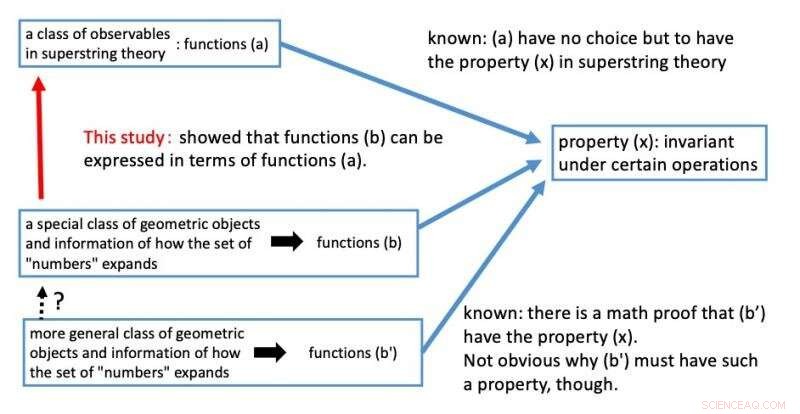
Figur 3. Sammanfattning av denna studie. Kredit:Kavli IPMU
Det bör noteras att resultatet ovan erhålls endast för den klass av geometriska objekt som kallas elliptiska kurvor med komplexa multiplikationer. Frågan är fortfarande öppen om funktionerna för mer generell klass av geometriska objekt (b) uttrycks i termer av observerbara i supersträngteorin (a).
Detaljer om denna studie publicerades den 22 februari, 2019, i Kommunikationer i matematisk fysik .