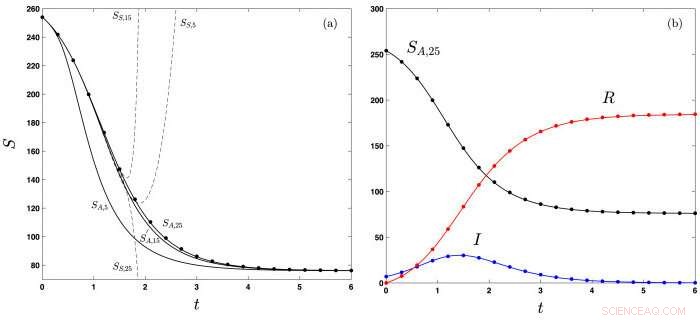
RIT-forskare utvecklade en lösning på SIR-epidemimodellen, som vanligtvis används för att förutsäga hur många människor som är mottagliga för, infekterad av, och återhämtade sig från virusepidemier. Figuren som visas ovan har utvecklats från uppskattningar av böldpestutbrottet 1966 i Eyam, England. Kredit:Rochester Institute of Technology
Rochester Institute of Technologys forskare har utvecklat en metod som de tror kommer att hjälpa epidemiologer att mer effektivt förutsäga spridningen av covid-19-pandemin. Deras nya studie, publicerad i Physica D:Icke-linjära fenomen , skisserar en lösning på SIR-epidemimodellen, som vanligtvis används för att förutsäga hur många människor som är mottagliga för, infekterad av, och återhämtade sig från virusepidemier.
Metoden skapades av Nathaniel Barlow, docent vid RIT:s institution för matematiska vetenskaper, och Steven Weinstein, chef för RIT:s institution för kemiteknik. De säger att genom att använda denna lösning till modellen, Epidemiologer kan snabbt förutse många olika scenarier för hur COVID-19 kan spridas baserat på en mängd olika variabler. Prognoser producerade av matematiska modeller hjälper offentliga tjänstemän att fatta politiska beslut om när de ska införa och häva restriktioner som syftar till att platta ut kurvan för infektionsfrekvensen.
De tillämpade matematikerna som utvecklade metoden sa att de var glada över att hitta ett sätt att tillämpa sina färdigheter för att hjälpa till att bekämpa pandemin.
"Jag var hemma och tänkte att jag på något sätt skulle vilja hjälpa till med allt som händer, " sa Barlow. "Vi såg en populär artikel där ute om SIR-modellen, såg att vår metod kunde påskynda processen och vi skrev snabbt uppsatsen. Vårt mål var att få bättre verktyg till experterna som bekämpar denna sjukdom."
Metoden byggde på lösningar som de tidigare utvecklat på väldigt olika problem inom termodynamiken, vätskemekanik och förutsäga ljusets banor runt svarta hål. De har arbetat mycket med studenter på grundutbildningen på dessa problem under de senaste sex åren och fann att lösningen på SIR-epidemimodellen hade en mycket liknande matematisk struktur. Även om författarna inte tidigare har arbetat inom området epidemiologi, deras tidigare arbete översattes sömlöst till detta nya område.
"Många gånger, det är vad vi som tillämpade matematiker gör – arbetar vid gränserna för fält där människor vanligtvis inte pratar, ", sade Weinstein. "Vi fyller en viktig funktion för att tillhandahålla algoritmer för att stödja vetenskaplig undersökning och förutsägelse. Tekniken vi har utvecklat här är generell för många olika områden."
Författarna arbetar nu med att visa hur deras metod kan tillämpas på mer komplexa modeller som SEIR-epidemimodellen, som liknar SIR-modellen men också förutsäger befolkningen som exponeras för en epidemi.