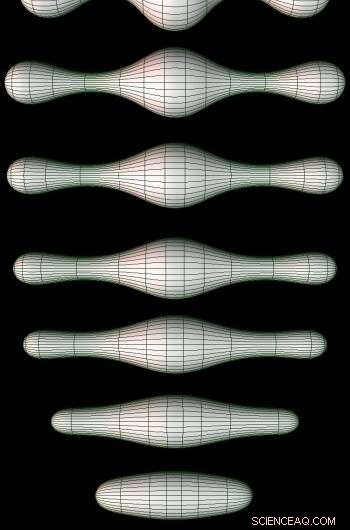
Servalstadierna av Ricci Flow på ett 2D-grenrör. Kredit:https://en.wikipedia.org/wiki/Ricci_flow
Differentialgeometri är studiet av rymdgeometri. Flera naturfenomen, från universell expansion till termisk expansion och sammandragning, kan komma ner till rumslig evolution. De två centrala gissningarna inom detta område, Hamilton-Tian gissningen och den partiella C 0 gissa, var olösta pussel i mer än 20 år.
"De flesta av stenarna på stranden är runda. De kan ha haft kanter och hörn först, men allt eftersom tiden går och tidvattnet ebbar ut och flyter, deras form kommer närmare och närmare perfektion och standard. Men hur perfekt utvecklingen än är, det kan fortfarande finnas några avvikelser, som kallas "singulariteter" i geometri."
"Hamilton-Tian-förmodan tyder på att det mesta av utrymmet är perfekt, medan storleken på "singulariteten" kan begränsas till ett lågdimensionellt utrymme, " sa professor Chen Xiuxiong, grundaren av Institutet för geometri och fysik, University of Science and Technology of China (USTC) vid den kinesiska vetenskapsakademin (CAS).
Prof Chen, tillsammans med prof. Wang Bing från USTC, först bevisade de två gissningarna.
Deras tidning var uppdelad i 123 sidor i två delar av, den första publicerades 2017 och den andra i år Journal of Differential Geometry , som också publicerade Hamiltons grundläggande arbete om Ricci-flödet efter en lång kurs på fem års utveckling av teorin och sex år av peer-review sedan dess första inlämning.
Detta arbete betonade teorin om svag kompakthet för icke-kollapsade Ricci-flöden. Den introducerade många innovativa tankar och metoder, som bidrog med långtgående implikationer inom området för geometrisk analys, speciellt för studier av Ricci-flöden.
Faktiskt, många andra verk har utvecklats baserat på den här artikeln. Till exempel, en ny lösning för stabilitet av Yaus gissningar baserad på strukturteorin för Ricci-flöden gavs av professor Chen, Prof. Wang och Dr. Sun Song från USTC med deras härledning publicerad i Geometri och topologi . Före det, de fick Oswald Veblen-priset i geometri för den första lösningen av stabiliteten i Yaus gissningar.
Teorin och metoderna som presenteras i denna artikel har också tillämpats i en serie arbeten av prof. Wang och hans medarbetare under de senaste åren.
Kärnidéerna i den här artikeln generaliserades till forskningen om medelkurvaturflöde av prof. Wang och prof. Li Haozhao, vem löste förlängningsproblemet, och resultatet publicerades i Uppfinningar Mathematicae .
Uppsatsen av prof. Wang, Dr Huang Shaosai och Dr Li Yu, "Om den regelbundna konvexiteten hos Ricci Shrinker Limit Spaces, " publicerad i Crelles tidning , har bevisat att gränsen för icke-kollapsade krympande Ricci-solitoner måste vara konformen definierad av prof. Chen och prof. Wang.
Dessutom, tidningen "Heat Kernel on Ricci Shrinkers, " publicerad i Variationskalkyl och partiella differentialekvationer av Prof Wang och Dr Li, utvecklat flera uppskattningar genom studiet av värmekärnan på Ricci-krympare och tillhandahållit "nödvändiga verktyg för att analysera korttidssingulariteter hos Ricci-flödena av allmän dimension."
Detta genombrott hedrades av tidskriftens recensent och vinnaren av Fields Metal, Prof. Simon Donaldson, vem sa, "Detta arbete är ett stort genombrott inom geometrisk analys, och det kommer utan tvekan att leda många andra relaterade forskningsprojekt."