
Många vetenskapliga studier håller inte i ytterligare tester. Kredit:A och N photography/Shutterstock.com
I en prövning av ett nytt läkemedel för att bota cancer, 44 procent av 50 patienter uppnådde remission efter behandling. Utan läkemedlet, bara 32 procent av tidigare patienter gjorde detsamma. Den nya behandlingen låter lovande, men är det bättre än standarden?
Den frågan är svår, så statistiker tenderar att svara på en annan fråga. De tittar på deras resultat och beräknar något som kallas ett p-värde. Om p-värdet är mindre än 0,05, resultaten är "statistiskt signifikanta" - med andra ord, sannolikt inte orsakas av en slumpmässig slump.
Problemet är, många statistiskt signifikanta resultat replikerar inte. En behandling som visar löften i en studie visar inte någon fördel alls när den ges till nästa patientgrupp. Detta problem har blivit så allvarligt att en psykologidagbok faktiskt förbjöd p-värden helt och hållet.
Mina kollegor och jag har studerat detta problem, och vi tror att vi vet vad som orsakar det. Gränsen för att hävda statistisk signifikans är helt enkelt för låg.
De flesta hypoteser är falska
The Open Science Collaboration, en ideell organisation med fokus på vetenskaplig forskning, försökte replikera 100 publicerade psykologiska experiment. Medan 97 av de första experimenten rapporterade statistiskt signifikanta fynd, endast 36 av de replikerade studierna gjorde.
Flera doktorander och jag använde dessa data för att uppskatta sannolikheten för att ett slumpmässigt valt psykologiska experiment testade en verklig effekt. Vi fann att bara cirka 7 procent gjorde det. I en liknande studie, ekonom Anna Dreber och kollegor uppskattade att endast 9 procent av experimenten skulle replikera.
Båda analyserna tyder på att endast en av 13 nya experimentella behandlingar inom psykologi - och förmodligen många andra samhällsvetenskaper - kommer att visa sig bli en framgång.
Detta har viktiga konsekvenser vid tolkning av p-värden, särskilt när de är nära 0,05.
Bayes -faktorn
P-värden nära 0,05 beror mer sannolikt på slumpmässiga slumpar än de flesta inser.
För att förstå problemet, låt oss återgå till vår imaginära drogrättegång. Kom ihåg, 22 av 50 patienter på det nya läkemedlet gick i remission, jämfört med i genomsnitt bara 16 av 50 patienter på den gamla behandlingen.
Sannolikheten att se 22 eller fler framgångar av 50 är 0,05 om det nya läkemedlet inte är bättre än det gamla. Det betyder att p-värdet för detta experiment är statistiskt signifikant. Men vi vill veta om den nya behandlingen verkligen är en förbättring, eller om det inte är bättre än det gamla sättet att göra saker.
Att få reda på, vi måste kombinera informationen i data med den tillgängliga informationen innan experimentet genomfördes, eller "tidigare odds". De tidigare oddsen speglar faktorer som inte mäts direkt i studien. Till exempel, de kan redogöra för det faktum att i 10 andra försök med liknande läkemedel, ingen visade sig vara framgångsrik.
Om det nya läkemedlet inte är bättre än det gamla läkemedlet, då berättar statistik att sannolikheten för att se exakt 22 av 50 framgångar i denna studie är 0,0235 - relativt låg.
Vad händer om det nya läkemedlet faktiskt är bättre? Vi vet faktiskt inte framgångsgraden för det nya läkemedlet, men en bra gissning är att det är nära den observerade framgångsgraden, 22 av 50. Om vi antar att, då är sannolikheten för att observera exakt 22 av 50 framgångar 0,133 - ungefär fem gånger mer sannolikt. (Inte nästan 20 gånger mer sannolikt, fastän, som du kanske gissar om du visste att p-värdet från experimentet var 0,05.)
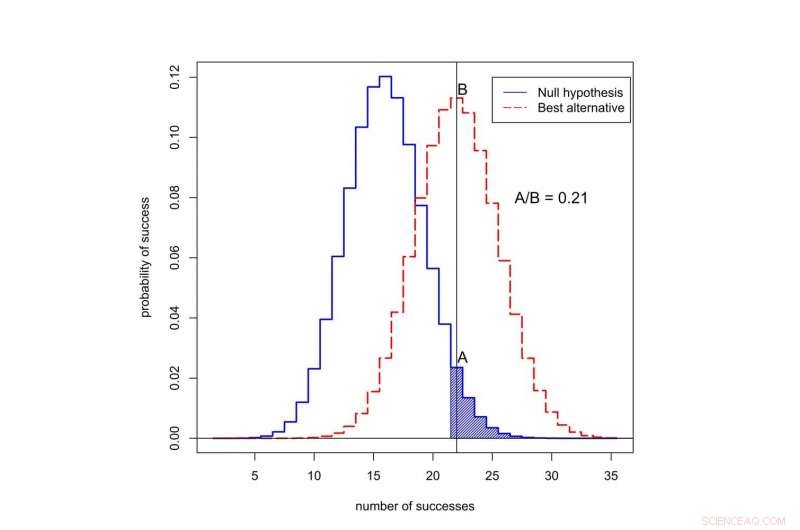
Vad är sannolikheten för att observera framgång i 50 försök? Den svarta kurvan representerar sannolikheter under nollhypotesen, När den nya behandlingen inte är bättre än den gamla. Den röda kurvan representerar sannolikheter när den nya behandlingen är bättre. Det skuggade området representerar p-värdet. I detta fall, förhållandet mellan sannolikheterna tilldelade 22 framgångar är A dividerat med B, eller 0,21. Upphovsman:Valen Johnson, CC BY-SA
Detta förhållande av sannolikheterna kallas Bayes -faktorn. Vi kan använda Bayes -satsen för att kombinera Bayes -faktorn med tidigare odds för att beräkna sannolikheten för att den nya behandlingen är bättre.
För argumentets skull, låt oss anta att endast 1 av 13 experimentella cancerbehandlingar kommer att visa sig vara en framgång. Det är nära det värde vi uppskattade för psykologiska experiment.
När vi kombinerar dessa tidigare odds med Bayes -faktorn, det visar sig att sannolikheten för att den nya behandlingen inte är bättre än den gamla är minst 0,71. Men det statistiskt signifikanta p-värdet på 0,05 tyder på exakt motsatsen!
Ett nytt tillvägagångssätt
Denna inkonsekvens är typisk för många vetenskapliga studier. Det är särskilt vanligt för p-värden runt 0,05. Detta förklarar varför en så stor andel statistiskt signifikanta resultat inte replikeras.
Så hur ska vi utvärdera inledande påståenden om en vetenskaplig upptäckt? I september, mina kollegor och jag föreslog en ny idé:Endast P-värden mindre än 0,005 bör betraktas som statistiskt signifikanta. P-värden mellan 0,005 och 0,05 bör bara kallas suggestiva.
I vårt förslag statistiskt signifikanta resultat är mer benägna att replikera, även efter att ha redogjort för de små tidigare oddsen som vanligtvis avser studier inom det sociala, biologiska och medicinska vetenskaper.
Vad mer, vi tycker att statistisk signifikans inte bör fungera som en gränslinje för publicering. Statistiskt suggestiva resultat - eller till och med resultat som i stort sett är otillräckliga - kan också publiceras, baserat på om de rapporterade viktiga preliminära bevis om möjligheten att en ny teori kan vara sann.
Den 11 oktober kl. vi presenterade denna idé för en grupp statistiker på ASA Symposium on Statistical Inference i Bethesda, Maryland. Vårt mål med att ändra definitionen av statistisk signifikans är att återställa den avsedda innebörden av denna term:att data har gett väsentligt stöd för en vetenskaplig upptäckt eller behandlingseffekt.
Kritik av vår idé
Alla håller inte med om vårt förslag, inklusive en annan grupp forskare som leds av psykologen Daniel Lakens.
De hävdar att definitionen av Bayes -faktorer är för subjektiv, och att forskare kan göra andra antaganden som kan förändra deras slutsatser. I den kliniska prövningen, till exempel, Lakens kan hävda att forskare kan rapportera remissionstakten på tre månader snarare än sex månader, om det gav starkare bevis för det nya läkemedlet.
Lakens och hans grupp tycker också att uppskattningen att endast ungefär ett av 13 experiment kommer att replikera är för lågt. De påpekar att denna uppskattning inte inkluderar effekter som p-hacking, en term för när forskare upprepade gånger analyserar sina data tills de hittar ett starkt p-värde.
Istället för att höja ribban för statistisk signifikans, Lakens -gruppen tycker att forskare bör fastställa och motivera sin egen statistiska signifikansnivå innan de utför sina experiment.
Jag håller inte med om många av Lakens -gruppens påståenden - och ur ett rent praktiskt perspektiv, Jag känner att deras förslag är ett icke -starkt. De flesta vetenskapliga tidskrifter ger inte någon mekanism för forskare att registrera och motivera sitt val av p-värden innan de utför experiment. Mer viktigt, Att låta forskare sätta sina egna bevisgränser verkar inte vara ett bra sätt att förbättra reproducerbarheten av vetenskaplig forskning.
Lakens förslag skulle bara fungera om tidskriftsredaktörer och finansieringsorgan i förväg kom överens om att publicera rapporter om experiment som inte har utförts baserat på kriterier som forskare själva har infört. Jag tror att detta inte kommer att hända när som helst inom en snar framtid.
Tills det gör det, Jag rekommenderar att du inte litar på påståenden från vetenskapliga studier baserade på p-värden nära 0,05. Insistera på en högre standard.
Denna artikel publicerades ursprungligen på The Conversation. Läs originalartikeln. 