
Kredit:John Griffiths/Flickr, CC BY-NC-ND
Arkeologer upptäckte nyligen en 600 år gammal dö som troligen användes för fusk. Träformen från medeltida Norge har två femmor, två fyror, en trea och en sexa, medan siffrorna ett och två saknas. Man tror att tärningen användes för att fuska i spel, snarare än att vara för ett spel som kräver den specifika konfigurationen av siffror.
I dag, tärningar som denna med saknade nummer kallas toppar och botten. De kan vara ett användbart sätt att fuska på om du är så benägen, även om de inte garanterar en vinst varje gång och de står inte upp för granskning från misstänkta motståndare (de behöver bara be om att få ta en titt och du kommer att bli upptäckt). Men det finns flera andra alternativ att fuska med tärningar också, och jag ska prata om några av dem här.
Det bör noteras att det är olagligt att använda dessa metoder i ett kasino och jag föreslår inte att du använder dem i sådana anläggningar – men det är en intressant titt på hur sannolikheter fungerar.
För ett rättvist dö, varje nummer har en på sex, eller 16,67 %, chans att dyka upp. När det gäller tärningen som hittades i Norge, siffrorna fyra och fem har dubbelt så stor sannolikhet att visas (eftersom det finns två av dem), så ha en av tre, eller 33,33 %, chans. Tabellen visar dessa sannolikheter.
Det krävs inte för mycket fantasi för att se hur toppar och underdelar kan användas till din fördel. Låt oss anta att vi spelar med två vanliga tärningar. Det finns 36 möjliga utfall men endast 11 möjliga totala värden som tärningarna kan producera. Till exempel, sex-fyra, fyra-sex och fem-fem summerar alla till tio.
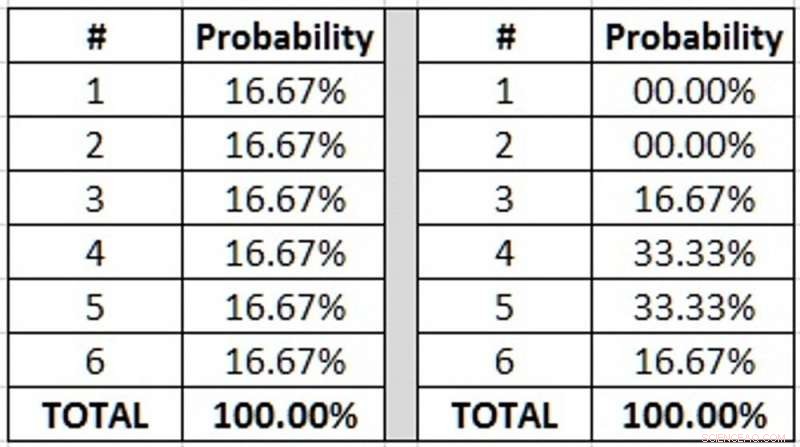
Sannolikheter för en rättvis tärning och en topp och botten tärning. Kredit:Graham Kendall
Om vi istället använde två övre och nedre tärningar med bara siffrorna ett, fyra och fem på dem, vi kan aldrig rulla totalt 11 eller 12 eftersom vi inte har en sexa för att göra den totalen. Liknande, vi kan aldrig få totalt tre eftersom vi inte har tvåor och enor. Men vi kan inte heller få någon kombination som skulle producera totalt sju, som annars skulle vara den mest sannolika totalen att visas med en sannolikhet på 16,67%. I en omgång craps finns det tillfällen då det kan vara riktigt dåligt att kasta en sjua. Så om du spelar med tärningar där en kombination av sju är omöjlig, du har en klar fördel.
Eftersom den här typen av toppar och bottnar tärningar inte kommer att passera ens en kortfattad, närmare granskning, de måste tas in i spelet en kort stund och sedan kopplas ut igen. Detta kräver att fusket är en expert på palming, vilket innebär att du kan dölja en uppsättning tärningar i din hand och sedan sätta dem i spel samtidigt som du tar bort de andra tärningarna.
Använd två tärningar, med samma tre siffror upprepade, kan vara för riskabelt så en fusk skulle förmodligen bara vilja byta in en enda tärning in i spelet. I vårt exempel, detta skulle innebära att man inte längre undviker totalt sju, vilket fortfarande skulle ha en sannolikhet på 16,67%. Men nu skulle summan av fem och sex också ha denna sannolikhet.
I craps är oddsen sådana att när du måste undvika en sjua, det är det nummer som mest sannolikt kommer att visas. Att byta in en enda tärning kan fortfarande minska husets chanser att vinna, genom att göra andra summor lika sannolika att visas.
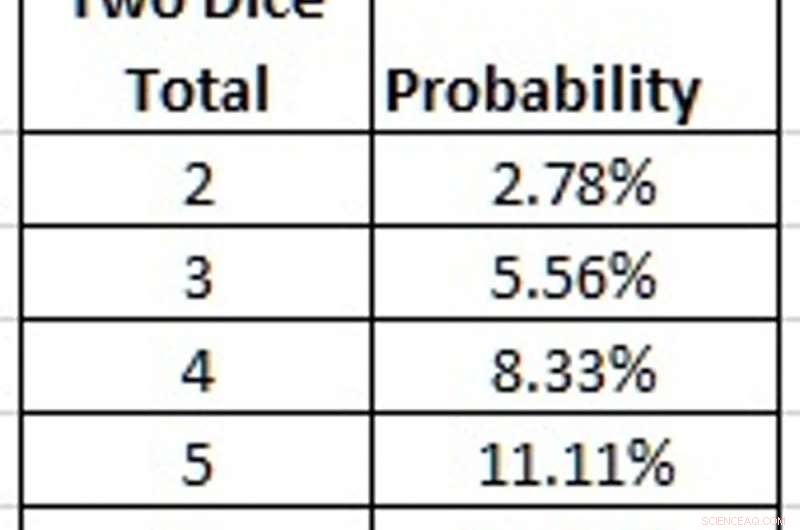
Sannolikheter för summan när två tärningar kastas. Kredit:Graham Kendall
Laddade tärningar
Laddade tärningar kan göra fusk svårare att upptäcka. Dessa kan ta ett antal olika former. Till exempel, några av fläckarna på ena sidan kan borras ut och hålen fyllas med en tung substans så det är mer sannolikt att formen landar med den här sidan nedåt. Om du skulle ta reda på nummer ett, detta betyder att siffran sex är mer sannolikt att visas, eftersom sexan alltid är på motsatt sida till den ena. Ett annat sätt att ladda en tärning skulle vara att något ändra dess form, så att det är mer troligt att det fortsätter rulla. Detta kanske bara ger en liten fördel, men det kan räcka för att tippa spelet till fuskets fördel.
Med toppar och underdelar är det lätt att veta sannolikheten för att olika totalsummor visas. Detta är inte fallet med laddade tärningar. Ett sätt att mäta sannolikheterna är att kasta tärningarna ett antal gånger (möjligen tusentals) och räkna ut vilka siffror som dyker upp och hur ofta. Om du vet att det är mindre sannolikt att sju dyker upp än med rättvisa tärningar, på lång sikt, det skulle vara en fuskfördel.
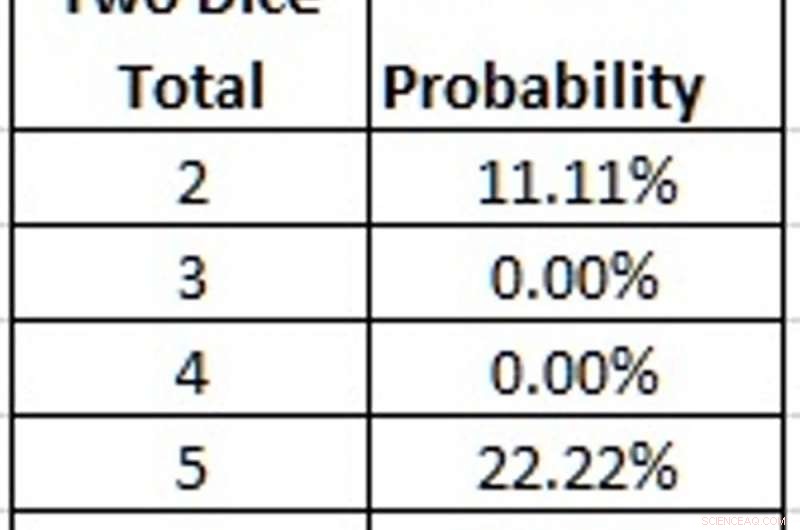
Hur man undviker att kasta en sjua med två övre och nedre tärningar. Kredit:Graham Kendall
Kontrollerade kast
Ett annat sätt att fuska kräver inte alls en orättvis tärning utan innebär att lära sig hur man kastar på ett mycket kontrollerat sätt. Detta kan innebära att man effektivt skjuter eller tappar tärningen så att önskat nummer visas. Om två tärningar används, den ena kan användas för att fånga den andra och stoppa den från att studsa. Om detta görs av en skicklig operatör, det är väldigt svårt att se.
Dominic LoRiggio, "Dice Dominator", kunde kasta tärningar på vad som verkade vara ett normalt sätt men så att de skulle landa på vissa nummer. Detta gjordes genom att förstå hur tärningarna färdas genom luften och kontrollera varje del av kasten. Det tog många (många, många) timmars träning för att fullända, men han kunde konsekvent vinna vid crapsbordet.
Många skulle anse att det LoRiggio gjorde som ett fördelsspel, vilket innebär att du använder reglerna till din fördel. Detta liknar korträkning i blackjack. Kasinon kanske inte gillar det, men du fuskar tekniskt sett inte – även om vissa kasinon kan försöka få dig att skjuta tärningarna på ett annat sätt om de misstänker att du gör kontrollerade kast.
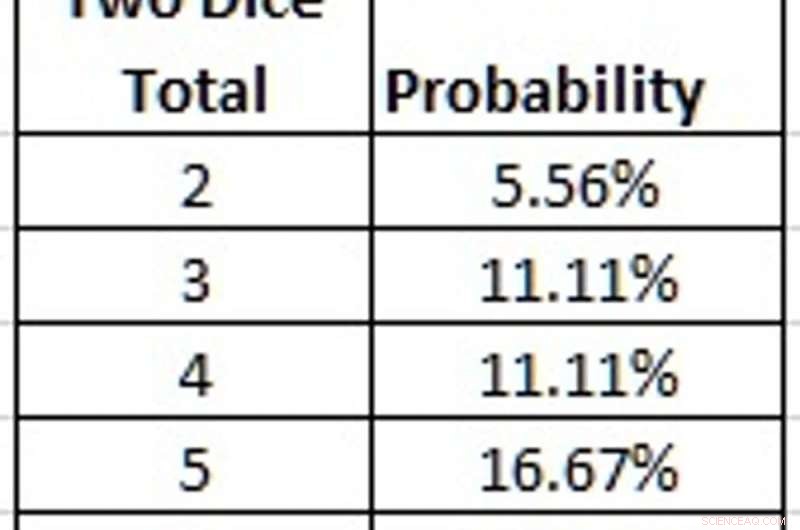
Sannolikheten för varje summa när en tärning har siffrorna ett, två, fyra upprepade. Kredit:Graham Kendall
Denna artikel publicerades ursprungligen på The Conversation. Läs originalartikeln. 