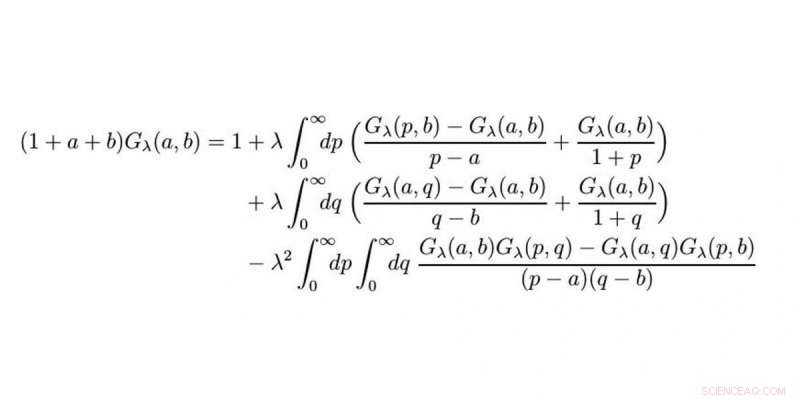
Den matematiska ekvationen. Kredit:WWU/Raimar Wulkenhaar
Efter 10 år, Prof. Raimar Wulkenhaar från University of Münsters Mathematical Institute och hans kollega Dr. Erik Panzer från University of Oxford har löst en matematisk ekvation som ansågs vara olöslig. Ekvationen ska användas för att hitta svar på frågor som ställs av elementarpartikelfysik. I denna intervju med Christina Heimken, Wulkenhaar ser tillbaka på utmaningarna när man letar efter formeln för en lösning och han förklarar varför arbetet ännu inte är avslutat.
Du arbetade med lösningen på ekvationen i 10 år. Vad gjorde denna ekvation så svår att lösa?
Det är en icke-linjär integralekvation med två variabler. En sådan ekvation är så komplex att du faktiskt tror att det omöjligt kan finnas någon formel för en lösning. Enbart två variabler är en utmaning i sig, och det finns inga etablerade tillvägagångssätt för att hitta en lösning för icke-linjära integralekvationer. Ändå, om och om igen under dessa 10 år fanns det glittrar av hopp och som ett resultat, och trots alla svårigheter, Jag trodde att det faktiskt var möjligt att hitta en explicit formel för en lösning – uttryckt genom kända funktioner.
Vad kan ekvationen användas till?
Det handlar om en matematisk förståelse av kvantfältsteorier. Dessa tillhör fysikområdet och spelar en roll i storskaliga experiment som de som utförs vid CERN. Syftet är att matematiskt beskriva elementarpartiklar, dvs de minsta kända komponenterna av materia. Men det här är så komplicerat att istället, imaginära partiklar beskrivs matematiskt som har vissa egenskaper hos de verkliga partiklarna. Förhoppningen är att de verkliga partiklarna en dag kan beskrivas med de metoder som etablerats på detta sätt.
Efter att ha arbetat med problemet i 10 år, du upplevde ett genombrott i år. Hur kom det sig?
Mot slutet av maj, Jag provade en idé som min doktorsexamen. studerande, Alexander Hock, gav den avgörande impulsen. Jag tog fram en ny ekvation – enklare än den tidigare – och började lösa den i loopar. Vad detta innebär är att du närmar dig lösningen steg för steg, dvs slinga för slinga, genom att beräkna den vänstra sidan av ekvationen i varje föregående steg och använda den för den högra sidan av ekvationen i nästa steg.
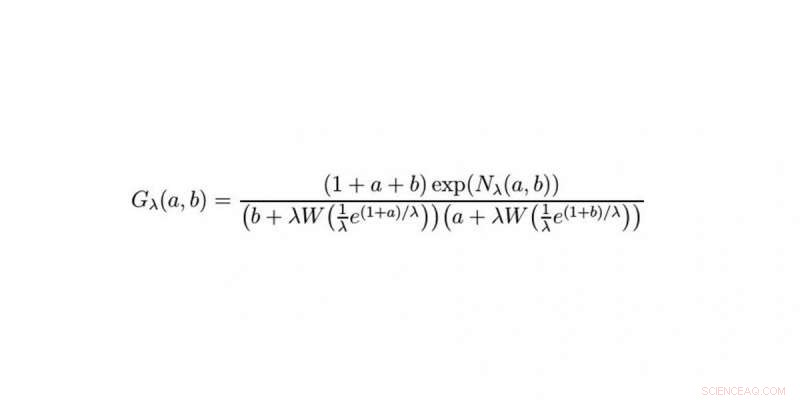
Lösningen. Kredit:WWU/Raimar Wulkenhaar
I den fjärde slingan fick jag räkna ut en summa av 46 integraler som innehöll bland annat polylogaritmer. Dessa polylogaritmer, som är några av de mer krävande funktionerna, blev mer komplicerat i varje slinga. Jag hade tur i det, kortfattat, nästan allt avbröts, och det som återstod var bara en kort summa potenser av normala logaritmer. Jag insåg direkt att det fanns skatter att hitta här.
Den femte slingan var inte så lätt att lösa – men återigen hade jag tur. Under en sommarskola i de franska alperna fick jag möjlighet att prata med experter om sådana funktioner. En av dessa experter var Dr Erik Panzer från University of Oxford. Han hade skrivit ett datorprogram om hyperlogaritmers symboliska matematik och han gav stöd. Över en natt beräknade det här programmet min ekvation fram till den sjunde slingan. Det bekräftade mina resultat fram till den fjärde slingan, och efter den fjärde slingan fortsatte miraklet – allt kunde brytas ner i normala logaritmer. Ett mönster började växa fram!
Vad betyder det?
Kanske minns du Pascals triangel från din skoltid, med de binominala koefficienterna? I triangeln, varje tal som anges på en rad i triangeln är summan av de två siffror som anges ovanför den. Och det är just en sådan triangulär struktur som vi hittar i våra slingor – om än mer komplicerad än i Pascals triangel.
Den 9 juni, slingor åtta och nio avslutades. Och så kom det som kanske var det viktigaste ögonblicket. Erik Panzer dechiffrerade en så kallad rekursiv formel, som genererar varje sista linje i triangeln från linjen ovanför den, och som därmed gör det möjligt för oss att extrapolera från det kända till det okända.
Vad gick igenom ditt sinne i detta ögonblick?
En av de saker jag trodde var, "Ingen kan vara så lycklig." Jag insåg att vi skulle lösa ekvationen. Vid vår kvällsmåltid fanns det en flaska vin till vårt bord...
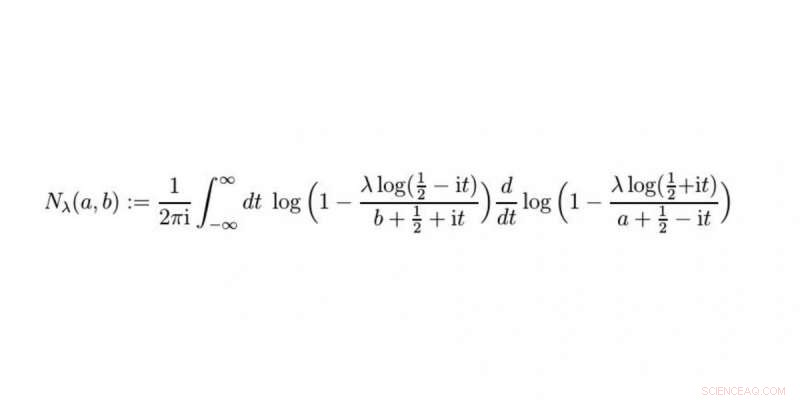
Nielsen-funktionen är en del av lösningen. Prof. Raimar Wulkenhaar och Dr. Erik Panzer upptäckte denna nya funktion under sitt arbete. Kredit:WWU/Raimar Wulkenhaar
… innan du kom tillbaka till jobbet.
Ja. Dagen efter lyckades jag reducera en del av ekvationen till en enkel serie av derivator. Initialt, resten verkade vara svårt. Inte förrän sent på kvällen kom jag på idén att använda Cauchy-formeln för att lösa det. Jag ställde min väckarklocka på 5:30 nästa morgon och provade den direkt. Det fungerade vid första försöket, och i nästa steg träffade jag en formel som jag ofta hade sett. Jag visste att det skulle lösas genom att använda Lambert W-funktionen. Några minuter senare fick jag ett mejl från Erik Panzer:även han hade tänkt på Lambert-funktionen, men på en helt annan väg. Som ett resultat, vi uppnådde något som inte hade varit genomförbart på 10 år:lösningen av integralekvationen som beskriver modellen för en kvantfältteori. Det var bara otroligt.
Man använder sig av idéer och metoder utvecklade av matematiker på 1700-talet som nästan helt glömts bort nuförtiden.
Dessa gamla formler hjälpte oss mycket. Lambert W-funktionen, som är en elementär del av vår lösning, är uppkallad efter den schweiziske matematikern Johann Heinrich Lambert. Denna ekvation dyker upp i ett stort antal helt olika frågor. På grund av bristande medvetenhet om Lamberts grundarbete, Lambert-funktionen uppfanns om och om igen, och det etablerades som standard först 1993. Vi använde också Lagrange-Bürmann-formeln, som hjälpte oss att lösa en integral med hjälp av Lambert-funktionen, samt Cauchy-formeln. I allmänhet, matematik har mycket respekt för sina förfäder. Namn som Euler, Lambert, Lagrange, Cauchy, Gauss och Hilbert citeras med största erkännande för sina prestationer. Men det finns två moderna verktyg jag inte skulle vilja vara utan:Wikipedia och datoralgebra. Du kan hitta omfattande information på Wikipedia som täcker välkända – och mindre kända – matematiska strukturer och funktioner. Datorer kan lösa ekvationer ojämförligt snabbare än för hand, och utan att göra några fel
Vad är nästa steg?
En ny funktion uppstår i vår lösning som vi har döpt till Nielsen-funktionen. När vi har förstått det bättre och har räknat ut till exempel hur det förhåller sig till andra kända funktioner, vi kommer att lämna in vårt arbete – som är fritt tillgängligt online som förtryck – för publicering i en facktidskrift med referentgranskning.
Efter det skulle jag vilja fortsätta ett arbete som jag har varit engagerad i sedan 2002 med min kollega professor Harald Grosse från Wien. Den behandlar en kvantfältteori för matematiska partiklar. Vi kommer nu att kunna förstå denna modell fullt ut med hjälp av den ekvation vi har löst.