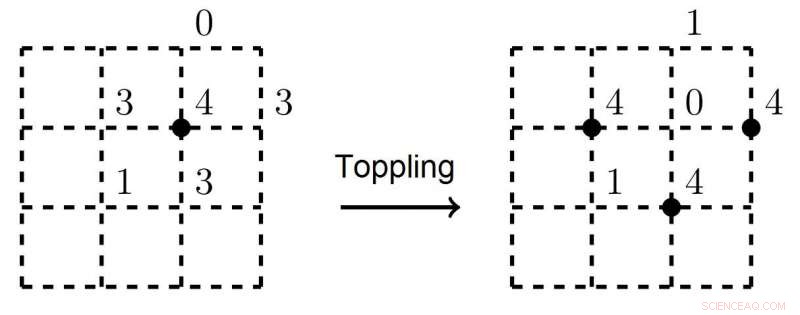
Den svarta pricken på den vänstra figuren markerar en instabil vertex. Efter en lavin, tre närliggande hörn blir instabila och kommer att kollapsa Kredit:Nikita Kalinin, Högre Handelshögskolan - Sankt Petersburg
En internationell grupp av forskare (första författaren är Nikita Kalinin, Högre Handelshögskolan – Sankt Petersburg, den sista författaren är Ernesto Lupercio, CINVESTAV, Mexiko) har presenterat den första kontinuerliga modellen som beskriver självorganiserad kritikalitet. Den föreslagna lösningen är enklare och mer universell än den klassiska sandhögmodellen. Den integrerar områden så avlägsna från varandra som ekonomi, utvecklingsbiologi, och gravitation i samband med tropisk geometri. Tidningen publicerades i Proceedings of the National Academy of Sciences .
Ett system sägs vara i ett kritiskt tillstånd om en yttre kraft, hur liten som helst, kan ge en lavineffekt som orsakar en förändring i systemets beteende. Dessa inkluderar fasövergångar:När en enda iskristall kommer fram i vatten kylt till noll grader Celsius, en iskluster kommer omedelbart att börja bildas.
Det finns vissa dynamiska system som tenderar mot ett kritiskt tillstånd - jordbävningar är ett illustrativt exempel. Medan en viss temperatur och tryck krävs för att vatten ska frysa, inga exakta parametrar behöver uppfyllas för att en jordbävning ska inträffa. Den främsta orsaken till jordbävningar är den kontinuerliga rörelsen av tektoniska plattor, och att förutsäga det exakta ögonblicket när systemet kommer att uppnå ett kritiskt tillstånd och producera en lavin är praktiskt taget omöjligt.
Många forskare har försökt lösa mysteriet med jordbävningar. I mitten av 1900-talet, Amerikanska seismologer Gutenberg och Richter visade ett samband mellan magnituden och det totala antalet jordbävningar i en viss region. Detta samband beskrivs av potenslagen uttryckt som en rät linje på en dubbel logaritmisk skala.
Fenomen som delar denna egenskap har sedan dess hittats inom geofysiken, kosmologi, ekonomi, riskhanteringsteori och andra områden. Alla kan beskrivas med teorin om självorganiserad kritikalitet (SOC).
Konceptet SOC introducerades av Per Bak, Chao Tang och Kurt Wiesenfeld 1987. I deras framstående tidning, de lade fram det arketypiska exemplet på ett SOC-system:Sandpile Model. Föreställ dig ett fyrkantigt rutnät med sandkorn i vart och ett av dess hörn, där nya korn faller på nätet med en viss frekvens. Det antas att om det inte finns mer än tre sandkorn i varje vertex, systemet förblir stabilt. Men så snart ett fjärde sandkorn faller på toppen av en vertex, det välter, och sanden glider nerför denna topp och omfördelas till närliggande hörn. Ställningen kommer att fortsätta i en lavin tills systemet återgår till jämvikt. Fysikernas nyckelupptäckt var att antalet hörn som faller (dvs storleken på det kollapsade området) uppfyller en kraftlagsfördelning.
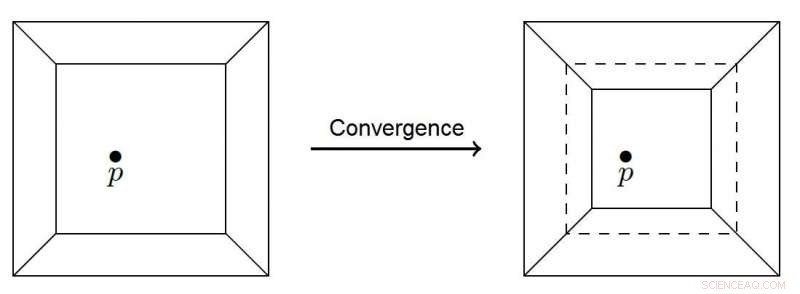
Polygon som konvergerar till en punkt. Kredit:Nikita Kalinin, Högre Handelshögskolan - Sankt Petersburg
Sandhögmodellen har länge varit den klassiska modellen som beskriver SOC. Dock, den beskriver dynamiken i kritiska system endast på fenomenologisk nivå och kan inte användas för att simulera en jordbävning eller förutsäga beteendet hos en riktig sandhög.
"Den gamla sandhögsmodellen, är rent kombinationsmässigt, skiljer sig något från matematikens stora värld. Vår modell är ett steg framåt, eftersom den har alla fördelar med sandhögmodellen, men den är också geometrisk och kontinuerlig, gör det mycket lättare att använda, " förklarar författaren Nikita Kalinin, senior forskare vid HSE International Laboratory of Game Theory and Decision Making. "Vi har visat att kraftlagskorrelationer kan erhållas i ett kontinuerligt system som inte är en cellulär automat med hjälp av tropisk geometri, som har många tillämpningar idag."
"Tropisk geometri är en gren av geometrin från det tjugoförsta århundradet inspirerad av klassisk algebraisk geometri som har blomstrat på grund av sina kopplingar till många vetenskapsområden, främst strängteori, " säger Dr. Ernesto Lupercio från CINVESTAV.
Istället för rutnätet som används i den klassiska sandhögmodellen, den nya modellen för tropisk sandhög betraktar en tropisk kurva – en plan graf med rätlinjiga kanter – innesluten i en kvadrat. Kurvan delar in kvadraten i polygonala områden, var och en innehåller en slumpmässigt vald uppsättning punkter. När en ny punkt läggs till, den tropiska kurvan försöker passera genom den, och det polygonala området som innehåller spetsen dras samman via en parallell överföring av dess kanter. Så snart en av kanterna träffar punkten, processen stannar. En ny punkt läggs sedan till, och det börjar om igen. Den föregående punkten kan vara borta från kurvan igen, och systemet kommer att börja röra sig mot det.
Denna konvergensprocess är en ändlig variant av att lägga sandkorn till en sandhög. I den nya modellen, lavinstorleken motsvarar det område som svepas av de konvergerande regionerna i processen som initieras genom att lägga till en slumpmässig punkt. Forskarna hoppas att deras modell kommer att hjälpa till att klargöra sambanden mellan olika fenomen som manifesterar SOC-egenskaper.
"Vi kan observera likheter i olika fenomen sett genom matematikens lins. Tropisk geometri har tillämpningar inom strängteorin, ekonomi och utvecklingsbiologi. Värdet av vårt arbete ligger i att hitta kopplingar på oväntade platser. Det betyder att de metoder som tillämpas på ett område kan tillämpas på ett annat. Du behöver bara ta nästa steg, säger Kalinin.