
Rubiks kub i löst tillstånd. Kredit:Mike Gonzalez (TheCoffee)
Rubiks kub har varit ett av världens favoritpussel i 40 år. Flera olika metoder har utarbetats för att lösa det, som förklaras i otaliga böcker. Expert "speedcubers" kan lösa det på några sekunder.
Förutom sådana bedrifter av häpnadsväckande skicklighet, det finns många fascinerande matematiska frågor relaterade till Rubiks kub. En rörelse av kuben består av att rotera en av de sex ytorna med antingen 90, 180, eller 270 grader. En svindlande 43, 252, 003, 274, 489, 856, 000 möjliga tillstånd kan erhållas genom att tillämpa sekvenser av drag till det lösta tillståndet.
Trots denna komplexitet, det visades 2010 att Rubiks kub alltid kan lösas i 20 drag eller färre, oavsett ursprungstillstånd. Detta nummer kallas "Guds nummer, " eftersom alla kända lösningsmetoder som används av människor vanligtvis använder betydligt fler rörelser än detta optimala värde.
Men hur är det med den motsatta frågan:hur många drag krävs för att förvränga en löst kub? Vid första ögonkastet, det här låter som en mycket lättare fråga än att beräkna Guds nummer. Trots allt, till skillnad från att lösa en kub, att förvränga kräver ingen som helst skicklighet.
Liknande frågor har besvarats framgångsrikt för kortblandning. Ett känt exempel är 1990 års studie av "riffle shuffle" av matematikerna Dave Bayer och Perci Diaconis. En kortlek definieras som "blandad" om dess ordning är slumpmässig, med varje möjlig ordning har samma sannolikhet att dyka upp. Bayer och Diaconis visade att sju riffelblandningar är nödvändiga och tillräckliga för att ungefär blanda en standardlek med spelkort.
Förra året, matematiker publicerade en liknande studie av 15-pusslet, som består av en 4x4 kvadrat fylld med 15 skjutbara plattor och ett tomt utrymme.

Fickkub i förvrängt tillstånd. Kredit:Mike Gonzalez (TheCoffee)
Vad betyder det att en kub förvrängs?
En typisk person som försöker krypa ihop en Rubiks kub skulle upprepade gånger utföra slumpmässiga rörelser på den. Den resulterande slumpmässiga sekvensen av tillstånd är ett specialfall av vad matematiker kallar en Markov-kedja. Nyckelegenskapen är att givet det nuvarande tillståndet, sannolikheten för vad nästa tillstånd kommer att vara beror inte på något av de tidigare tillstånden.
Att tillämpa teorin om Markov-kedjor på kubförvrängning, det följer att när antalet slumpmässiga drag ökar, sannolikheten att vara i något speciellt av de möjliga tillstånden blir närmare och närmare 1/43, 252, 003, 274, 489, 856, 000. Matematiker kallar detta en "likformig sannolikhetsfördelning, " eftersom varje möjligt tillstånd inträffar med samma sannolikhet.
Efter ett givet antal slumpmässiga drag, kubens tillstånd kommer att vara slumpmässigt, men dess sannolikhetsfördelning kommer inte att vara exakt enhetlig; vissa stater kommer att vara mer benägna att inträffa än andra.
Låta d(t) beskriv hur mycket sannolikhetsfördelningen efter t slumpmässiga drag skiljer sig från den enhetliga sannolikhetsfördelningen. Som antalet slumpmässiga drag ( t ) ökar, värdet av d(t) kommer att minska. Kuben som förvrängs motsvarar d(t) vara liten.
Markov-kedjan Monte Carlo
I teorin om Markov-kedjor, denna minskning i d(t) kallas "blandning". Förutom kortblandning och pusselförvrängning, teorin om Markov-kedjeblandning har också mycket seriösa praktiska tillämpningar. Ett av de viktigaste beräkningsverktygen inom modern vetenskap och teknik är Monte Carlo-metoden. Den här metoden, som det berömda kasinot som det är uppkallat efter, förlitar sig i grunden på slumpen. I huvudsak, den försöker ungefär lösa svåra matematiska problem med hjälp av flera slumpmässiga gissningar.
I praktiken, Markov-kedjor används ofta för att producera dessa slumpmässiga tillstånd. För att förstå noggrannheten i dessa Markov-kedja Monte Carlo-metoder, nyckeluppgiften är att uppskatta hur snabbt d(t) minskar som t ökar.
Fickkuben
Att studera förvrängningsproblemet för standarden 3x3x3 Rubik's Cube är för närvarande en fascinerande olöst utmaning. Dock, det blir ganska hanterbart om vi riktar vår uppmärksamhet mot en mindre 2x2x2 version, kallas fickkuben.
I denna kub, kant- och mittstyckena saknas och endast hörnstyckena finns kvar. Fickkuben har bara 3, 674, 160 möjliga tillstånd, och dess Guds nummer är bara 11.
I grafen nedan, vi plottar d(t) för fickkuben. Efter 11 drag, d(t) är fortfarande mycket stor, vid 0,695. Det första värdet av t som ger a d(t) värde under 0,25 (ofta kallat "blandningstiden" i Markovs kedjeteorin) är 19. Efter 25 drag d(t) är 0,092; efter 50 drag är det 0,0012; och efter 100 drag är det 0,00000017.
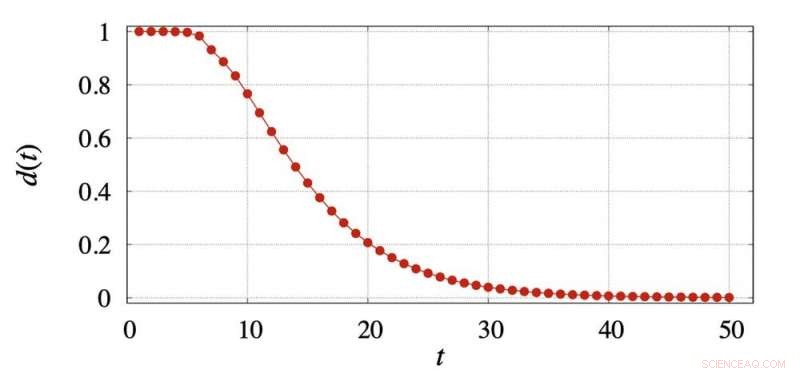
Avståndet mellan fickkubfördelningen från uniform efter t flyttar. Kredit:Eric Zhou
Så hur många drag ska du använda för att helt förvränga en fickkub? Svaret beror på hur liten du vill d(t) att vara. Dock, det är säkert sant att Guds antal drag är otillräckligt. Som ett absolut minimum, man bör inte använda färre än 19 drag. Ytterligare detaljer, inklusive kod att beräkna d(t) , finns här.
Och naturligtvis, när du väl har förvrängt din kub, allt som återstår att göra är att lösa det igen.
Den här artikeln är återpublicerad från The Conversation under en Creative Commons-licens. Läs originalartikeln. 